EASY
CAT
IMPORTANT
Earn 100

An equilateral triangle plate is to be cut into n number of identical small equilateral triangle plates. Which of the following can be a possible value of n ?

100% studentsanswered this correctly

Important Questions on Measurement

MEDIUM
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 4 - Measurement>Benchmarking Test 4>Q 8
In an isosceles trapezium ABCD,Pand Q are the mid-points of diagonals BD and AC, respectively, and PQ=4 cm. The perpendicular drawn from A on BD is 5 cmand that from C on BD is 6 cm and each of the diagonals measure 8 cm. Find the length of the sides of AB and CD, given that the height of the trapezium is 4 cm.
EASY
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 4 - Measurement>Benchmarking Test 4>Q 15

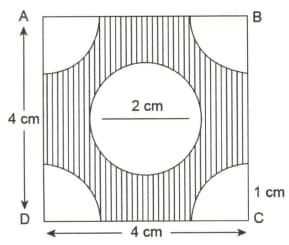
In the figure given below, ABCD is a square of side length 4 units which has four symmetric cuts at all its corners. Find the area of the shaded portion.

 Question Image

MEDIUM
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 4 - Measurement>Benchmarking Test 4>Q 16
If 9p2+4,(2p+7), and 8p2-1 are the lengths of three sides of a triangle (p>1). Which of the following cannot be a value of p ?
HARD
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 4 - Measurement>Benchmarking Test 4>Q 17
AB is a line segment and P is its mid-point. Semicircles are drawn with AP, PB, and AB as diameters on the same side of the line AB. A circle is drawn to touch all the three semicircles. Find the radius of this circle.
EASY
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 4 - Measurement>Benchmarking Test 4>Q 27
An octagon is inscribed in a circle. One set of alternate vertices forms a square of area 5 units. The other set forms a rectangle area of 4 units. What is the maximum possible area for the octagon (in sq. units)?
EASY
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 4 - Measurement>Benchmarking Test 4>Q 28
What is the largest number of the quadrilaterals formed by four adjacent vertices of an convex polygon of n sides that can have an inscribed circle?
EASY
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 4 - Measurement>Benchmarking Test 4>Q 29
There are two circles with centres at A and B, respectively. The circle with centre A has a radius of 8 units and the circle with centre B has a radius of 6 units and the distance of AB is 12 units. Both the circles meet at points P and S. A line through P meets the circles again at Q and R (with Q on the larger circle) in such a way that Q P=P R. Find the length of Q P.
HARD
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 4 - Measurement>Benchmarking Test 4>Q 30
A circle of 4 units is taken. Now, n circles of the same radii are inserted in this circle (1≤n≤10, where n is a natural number) in such a way that they are encompassing the maximum possible areas of the circle and are inside the bigger circle along its circumference. (Obviously, for n=1, radius of the inside circle will be same as the radius of the outside circle. Similarly, for n=2, radius of the inside circle will be half of the outside bigger circle and so on.) For how many values of n, radius of the circle will be an integer?