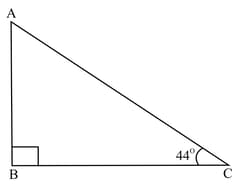
An exterior angle of a triangle is of measure 113 and one of its interior opposite angles is of 25 Find the measure of the other interior opposite angle in degree

EASY

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

The ratio of angles in a triangle is

1 : 2 : 3

, then the largest angle is

HARD

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

In the figure, if $O P ∥ R S, ∠ O P Q = 110 °$ and $∠ Q R S = 130 °$ , then $∠ P Q R$ is equal to

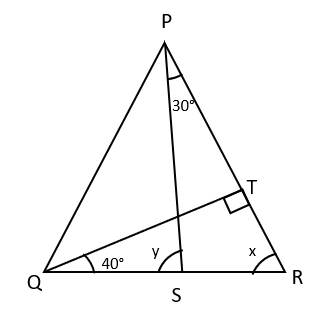
Question Image

MEDIUM

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

In the figure if $Q T ⊥ P R, ∠ T Q R = 40 °$ and $∠ S P R = 30 °$ . Then the value of $x$ and $y$ will be

Question Image

HARD

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

Let

A B

be a chord of a circle with centre

O .

Let

C

be a point on the circle such that

∠ A B C = 30 °

and

O

lies inside the triangle

A B C

. Let

D

be a point on

A B

such that

∠ D C O = ∠ O C B = 20 ° .

Find the measure of

∠ C D O

in degrees.

MEDIUM

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

In

∆ A B C, B E

and

C D

are the perpendiculars on sides AC and AB, respectively and intersect each other at O. The bisectors of

∆ O B C

and

∆ O C B

meet at P. If

∆ B P C = 146 °

, then what is the measure of

∠ A

?

HARD

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

Let

A B C

be a triangle and let

Ω

be its circumcircle. The internal bisectors of angles

A, B

and

C

intersect

Ω

at

A_{1}, B_{1}

and

C_{1},

respectively, and the internal bisectors of angles

A_{1}, B_{1}

and

C_{1}

of the triangle

A_{1} B_{1} C_{1}

intersect

Ω

at

A_{2}, B_{2}

and

C_{2},

respectively. If the smallest angle of triangle

A B C

is

40 °,

what is the magnitude of the smallest angle of triangle

A_{2} B_{2} C_{2}

in degrees?

HARD

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

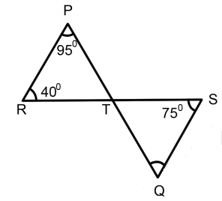
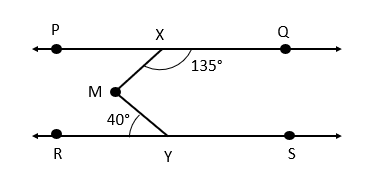
In the given figure, if $P Q ∥ R S$ , $∠ M X Q = 135 °$ and $M Y R = 40 °$ , then the value of $∠ X M Y$ will be
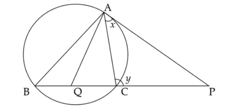
Question Image

EASY

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

In the figure, chord $B C$ is extended to $P$ . Tangent from $P$ to the circle is $P A$ . $A Q$ is the bisector of $∠ B A C$ . If $∠ P A C = x$ and $∠ P C A = y$ , then prove that $∠ B A C = y - x$ .

Question Image

MEDIUM

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

If in a

∆ A B C, A B = A C

and

∠ A = 70 °

, then

∠ B

is equal to

MEDIUM

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the value of vertex angle will be -

HARD

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

Let

A B C

be a triangle such that

A B = A C

. Suppose the tangent to the circumcircle of

A B C

at

B

is perpendicular to

A C

. Find

∠ A B C

measured in degrees.

HARD

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

$A B C D$ is a quadrilateral in which $A B = A C, A D = C D = 13 cm, ∠ B A C = 20 ° and ∠ A D C = 100 °$ . If $B C = 12 cm$ , then $A B$ is equal to

EASY

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

A B

is a diameter of a circle and

P

is any point on the circle if

∠ P A B = 30 °

, find the value of the

∠ P B A

in degrees.

MEDIUM

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

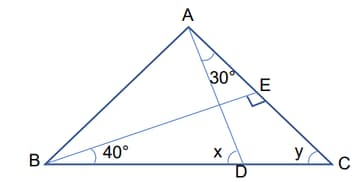
In the given figure, if $B E ⊥ A C$ , $∠ EBC = 40^{\circ}$ and $∠ DAC = 30^{\circ}$ , then the value of $∠ x$ and $∠ y$ are:

Question Image

EASY

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

In the figure, $∠ B = 90 °, ∠ C = 44 °$

Question Image

What is the measure of $∠ A$ ?

EASY

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

Question Image

$A B C D$ is a parallelogram where $A B = 8 cm, A D = 4 cm$ and $∠ B = 120 °$ . What is the value of $∠ A$ ?

EASY

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

In the figure, chord $B C$ is extended to $P$ . Tangent from $P$ to the circle is $P A$ . $A Q$ is the bisector of $∠ B A C$ . Prove that $∠ P A Q = \frac{y + x}{2}$

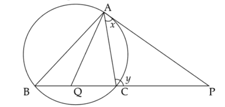
Question Image

MEDIUM

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

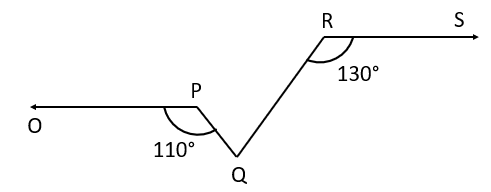
In the given figure, if line $P Q$ and the line $R S$ intersect at $T$ such that $∠ P R T = 40 °$ , and $∠ R P T = 95 °$ and $∠ T S Q = 75 °$ , then the value of $∠ S Q T$ will be

Question Image

EASY

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

Each exterior angle of a regular polygon is less than

40 °

and the sum of its interior angles is less than

1980 °

, if

N

is the number of sides of the polygon, then the number of possible values of

N

is

HARD

Mathematics>Geometry>Geometry>Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.

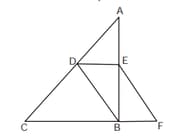
In the adjoining figure, $A B C$ is right-angled at $B$ . The point $D$ is on $A C$ such that $B D = B C$ and $B D E F$ is a parallelogram. If $∠ B E F = 10 °$ , then $∠ A D E$ is equal to.

Question Image

An exterior angle of a triangle is of measure $113 °$ and one of its interior opposite angles is of $25 °$ . Find the measure of the other interior opposite angle (in degree).

Important Questions on Geometry

Learn and Prepare for any exam you want !

An exterior angle of a triangle is of measure 113° and one of its interior opposite angles is of 25° . Find the measure of the other interior opposite angle (in degree).

Important Questions on Geometry

Learn and Prepare for any exam you want !

An exterior angle of a triangle is of measure $113 °$ and one of its interior opposite angles is of $25 °$ . Find the measure of the other interior opposite angle (in degree).