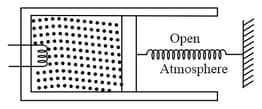
An ideal monatomic gas is confined in a cylinder by a spring-loaded massless piston of cross-section $8\times {10}^{-3} {\mathrm{m}}^2$. The piston can slide on the walls of the cylinder without any friction. Initially, the gas is at $300 \mathrm{K}$ and occupies a volume of $2.4\times {10}^{-3} {\mathrm{m}}^3$ and the spring is in its relaxed position. Now, gas is slowly heated by a small electric heater and the piston moves out slowly by $0.1 \mathrm{m}$. Calculate the final temperature of the gas and the heat supplied by the heater. The force constant of the spring is $8000 \mathrm{N}/\mathrm{m}$ and atmospheric pressure is $1\times {10}^{5 }\mathrm{N}/{\mathrm{m}}^2$.

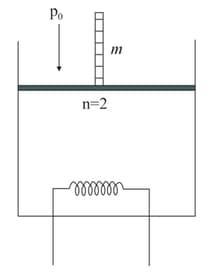
Two moles of an ideal monatomic gas are contained in a vertical cylinder of cross-sectional area $A$ as shown in the figure. The piston is frictionless and has a mass $m.$ At a certain instant, a heater starts supplying heat to the gas at a constant rate $q$ watt. Find the velocity of the piston under isobaric condition. All the boundaries are adiabatic in nature.

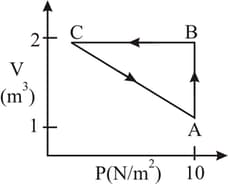
An ideal gas is taken through the cycle $A\to B\to C\to A$ as shown in the fig. If the net heat supplied to the gas in the cycle is $5 \mathrm{J},$ the work done by the gas in the process $C\to A$ is:

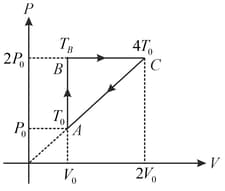
One mole of a gas is subjected to two process $AB$ and $BC$ one after the other as shown in the figure. $BC$ is represented by, $P{V}^{\mathrm{n}}=\text{constant}$. We can conclude that (where, $T=$temperature, $W=$work done by gas, $V=$volume and $U=$internal energy),

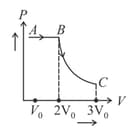
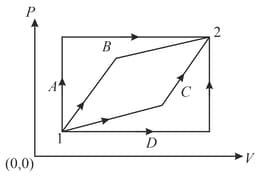
An ideal gas is taken from state $1$ to state $2$ through optional path $A, B, C$ and $D$, as shown in the $PV$ diagram. Let $Q, W$ and $U$ represent the heat supplied, work done and change in internal energy of the gas, respectively. Then,