EASY

Earn 100

Assertion: In a process if initial volume is equal to the final volume, work done by the gas is zero.

Reason: In an isochoric process work done by the gas is zero.

50% studentsanswered this correctly

Important Questions on Heat and Thermodynamics

HARD

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

Answer the following by appropriately matching the lists based on the information given in the paragraph.
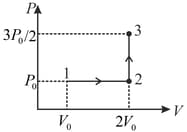
In a thermodynamics process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by

T Δ X,

where

T

is temperature of the system and

Δ X

is the infinitesimal change in a thermodynamic quantity

X

of the system. For a mole of monatomic ideal gas

X = \frac{3}{2} R l n (\frac{T}{T_{A}}) + R l n (\frac{V}{V_{A}}) .

Here,

R

is gas constant,

V

is volume of gas,

T_{A}

and

V_{A}

are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

	List I		List II
(I)	Work done by the system in process $1 \to 2 \to 3$	(P)	$\frac{1}{3} R T_{0} l n 2$
(II)	Change in internal energy in process $1 \to 2 \to 3$	(Q)	$\frac{1}{3} R T_{0}$
(III)	Heat absorbed by the system in process $1 \to 2 \to 3$	(R)	$R T_{0}$
(IV)	Heat absorbed by the system in process $1 \to 2$	(S)	$\frac{4}{3} R T_{0}$
		(T)	$\frac{1}{3} R T_{0} (3 + l n 2)$
		(U)	$\frac{5}{6} R T_{0}$

If the process carried out on one mole of monatomic ideal gas is as shown in figure in the

T

V

-diagram with

P_{0} V_{0} = \frac{1}{3} R T_{0},

the correct match is,

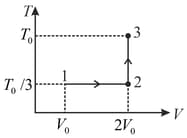
Question Image

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

A sample of

0.1 g

of water at

100^{o} C

and normal pressure

(1.013 \times 10^{5} N m^{- 2})

requires

54 cal

of heat energy to convert to steam at

100^{o} C

. If the volume of the steam produced is

167.1 cc,

the change in internal energy of the sample, is

HARD

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

T Δ X,

where

T

is temperature of the system and

Δ X

is the infinitesimal change in a thermodynamic quantity

X

of the system. For a mole of monatomic ideal gas

X = \frac{3}{2} R l n (\frac{T}{T_{A}}) + R l n (\frac{V}{V_{A}}) .

Here,

R

is gas constant,

V

is volume of gas,

T_{A}

and

V_{A}

are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

	Column - I		Column - II
(I)	Work done by the system in process $1 \to 2 \to 3$	(P)	$\frac{1}{3} R T_{0} l n 2$
(II)	Change in internal energy in process $1 \to 2 \to 3$	(Q)	$\frac{1}{3} R T_{0}$
(III)	Heat absorbed by the system in process $1 \to 2 \to 3$	(R)	$R T_{0}$
(IV)	Heat absorbed by the system in process $1 \to 2$	(S)	$\frac{4}{3} R T_{0}$
		(T)	$\frac{1}{3} R T_{0} (3 + l n 2)$
		(U)	$\frac{5}{6} R T_{0}$

If the process on one mole of monatomic ideal gas is as shown in the

P V

-diagram with

P_{0} V_{0} = \frac{1}{3} R T_{0},

the correct match is

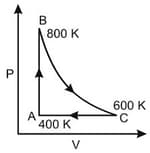
Question Image

HARD

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

The internal energy

(U)

, pressure

(P)

and volume

(V)

of an ideal gas are related as

U = 3 P V + 4 .

The gas is

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

One mole of diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperatures at A, B and C are 400 K, 800 K and 600 K respectively. Choose the correct statement :

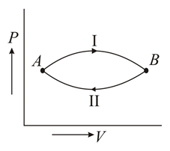
Question Image

EASY

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

A gas at state $A$ changes to state $B$ through path $I$ and $II$ shown in figure. The change in internal energy is $Δ U_{1}$ and $Δ U_{2}$ , respectively. Then

Question Image

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

The equation of state for a gas is given by

PV = nRT + α V

, where n is the number of moles and

α

is a positive constant. The initial temperature and pressure of one mole of the gas contained in a cylinder are T₀ and P₀ respectively. The work done by the gas when its temperature doubles isobarically will be :

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

An ideal gas in a cylinder is separated by a piston in such a way that the entropy of one part is

S_{1}

and that of the other part is

S_{2}

. Given that

S_{1} > S_{2}

. If the piston is removed then the total entropy of the system will be:

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

An ideal gas is taken reversibly around the cycle $a - b - c - d - a$ as shown on the T (temperature) - S (entropy) diagram

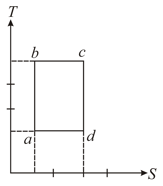
Question Image

The most appropriate representation of above cycle on a U (internal energy)-V (volume) diagram is

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

N

moles of diatomic gas in a cylinder is at a temperature

T

. Heat is supplied to the cylinder such that the temperature remains constant but

n

moles of the diatomic gas get converted into monoatomic gas. The change in the total kinetic energy of the gas is

HARD

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

The volume

V

of a given mass of monoatomic gas changes with temperature

T

according to the relation

V = K T^{\frac{2}{3}}

. The workdone when temperature changes by

90 K

will be

x R

. The value of

x

is
[

R

universal gas constant ]

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

An ideal monoatomic gas occupies a volume of

2 m^{3}

at a pressure of

3 \times 10^{6} Pa .

The energy of the gas is:

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

A monoatomic gas of mass

4.0 u

is kept in an insulated container. The container is moving with velocity

30 m s^{- 1}

. If the container is suddenly stopped then a change in temperature of the gas (

R =

gas constant) is

\frac{x}{3 R}

. Value of

x

is,

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

A thermodynamic system undergoes a cyclic process $A B C$ as shown in the diagram. The work done by the system per cycle is

Question Image

EASY

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

A container is divided into two chambers by a partition. The volume of first chamber is

4.5 litre

and second chamber is

5.5 litre

. The first chamber contain

3.0

moles of gas at pressure

2.0 atm

and second chamber contain

4.0

moles of gas at pressure

3.0 atm

. After the partition is removed and the mixture attains equilibrium, then, the common equilibrium pressure existing in the mixture is

x \times 10^{- 1} atm

. Value of

x

(nearest integer) is

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

The temperature of $3.00 mol$ of an ideal diatomic gas is increased by $40.0 ° C$ without changing the pressure of the gas. The molecules in the gas rotate but do not oscillate. If the ratio of change in internal energy of the gas to the amount of workdone by the gas is $\frac{x}{10} .$ Then the value of $x$ (round off to the nearest integer) is $_________.$

$($ Given $R = 8.31 J {mol}^{- 1} K^{- 1})$

EASY

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

A gas mixture contains monoatomic and diatomic molecules of

2

moles each. The mixture has a total internal energy of (symbols have usual meanings)

MEDIUM

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

A gas mixture consists of

2

moles of

O_{2}

and 4 moles of

Ar

at temperature

T

. Neglecting all vibrational modes, the total internal energy of the system is (

R

is universal gas constant)

EASY

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

An ideal gas is compressed to half of its initial volume by means of several processes. Which of the process results in the maximum work done on the gas?

EASY

General Science>Physics>Heat and Thermodynamics>First Law of Thermodynamics

2 kg

of a monoatomic gas is at a pressure of

4 \times 10^{4} N m^{- 2}

. The density of the gas is

8 kg m^{- 3}

. What is the order of energy of the gas due to its thermal motion?

Assertion: In a process if initial volume is equal to the final volume, work done by the gas is zero. Reason: In an isochoric process work done by the gas is zero.

Important Questions on Heat and Thermodynamics

Learn and Prepare for any exam you want !

Assertion: In a process if initial volume is equal to the final volume, work done by the gas is zero.

Reason: In an isochoric process work done by the gas is zero.