MEDIUM

Earn 100

Assertion: The specific heat at constant pressure is greater than the specific heat at constant volume i.e., $C_{P} > C_{V}$ .

Reason: In case of specific heat at constant volume, the whole of heat supplied is used to raise the temperature of one mole of the gas through $1 ° C$ while in case of specific of heat at constant pressure, heat is to be supplied not only for heating 1 mole of gas through $1 ° C$ but also for doing work during expansion of the gas.

50% studentsanswered this correctly

Important Questions on Thermodynamics

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

Consider two ideal diatomic gases

A

and

B

at some temperature

T

. Molecules of the gas

A

are rigid, and have a mass

m

. Molecules of the gas

B

have an additional vibrational mode and have a mass

\frac{m}{4}

. The ratio of the specific heats

{(C_{V}^{})}_{A} and {(C_{V}^{})}_{B}

of gas

A

and

B,

respectively is:

HARD

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

The specific heats,

C_{p}

and

C_{v}

of a gas of diatomic molecules,

A,

are given (in units of

J m o l^{- 1} K^{- 1}

) by

29

and

22,

respectively. Another gas of diatomic molecules,

B,

has the corresponding values

30

and

21 .

If they are treated as ideal gases, then:

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

Two moles of an ideal gas, with

\frac{C_{P}}{C_{V}} = \frac{5}{3}

, are mixed with three moles of another ideal gas

\frac{C_{P}}{C_{V}} = \frac{4}{3}

. The value of

\frac{C_{P}}{C_{V}}

for the mixture is

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

What will be the molar specific heat at constant volume of an ideal gas consisting of rigid diatomic molecules?

EASY

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

For a rigid diatomic molecule, the universal gas constant

R = n C_{P}

, where,

C_{P}

is the molar specific heat at constant pressure and

n

is a number. Hence,

n

is equal to

EASY

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

The values of

C_{p}

and

C_{v}

for a diatomic gas are respectively

(R = g a s

constant)

HARD

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

Consider a mixture of

n

moles of helium gas and

2 n

moles of oxygen gas (molecules taken to be rigid) as an ideal gas. Its

\frac{C_{P}}{C_{V}}

value will be:

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

The correct relation between the degrees of freedom

f

and the ratio of specific heat

γ

is:

EASY

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

An ideal gas has molecules with

5

degrees of freedom. The ratio of specific heats at constant pressure

(C_{p})

and at constant volume

(C_{V})

is:

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

When heat

Q

is supplied to a diatomic gas of rigid molecules, at constant volume its temperature increases by

∆ T

. The heat required to produce the same change in temperature, at a constant pressure is:

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

One mole of a monoatomic ideal gas undergoes a quasistatic process, which is depicted by a straight line joining points

(V_{0}, T_{0})

and

(2 V_{0}, 3 T_{0})

in a

V - T

diagram. What is the value of the heat capacity of the gas at the point

(V_{0}, T_{0}) ?

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

For a diatomic ideal gas in a closed system, which of the following plots does not correctly describe the relation between various thermodynamic quantities?

HARD

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

One gram mole of an ideal gas

A

with the ratio of constant pressure and constant volume specific heats

γ_{A} = \frac{5}{3}

is mixed with

n

gram moles of another ideal gas

B

with

γ_{B} = \frac{7}{5}

. If the

γ

for the mixture is

\frac{19}{13}

, then what will be the value of

n

EASY

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

One mole of

O_{2}

gas is heated at constant pressure starting at

27 ° C

. How much energy must be added to the gas as heat to double its volume?

EASY

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

The ratio of

\frac{C_{p}}{C_{v}}

for a diatomic gas is

EASY

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

For a gas

C_{P} - C_{V} = R

in a state

P

and

C_{P} - C_{V} = 1.10 R

in a state

Q, T_{P}

and

T_{Q}

are the temperatures in two different states

P

and

Q

, respectively. Then

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

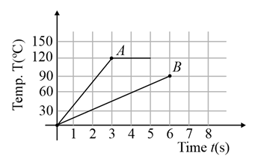
Two different metal bodies $A$ and $B$ of equal mass are heated at a uniform rate under similar conditions. The variation of temperature of the bodies is graphically represented as shown in the figure. The ratio of specific heat capacities is:

Question Image

MEDIUM

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

A cylinder with fixed capacity of

67.2

litre contains helium gas at STP. The amount of heat needed to raise the temperature of the gas by

20 ° C

is:
[Given that

R = 8.31 J m o l^{- 1} K^{- 1}]

EASY

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

C_{p} - C_{v} = \frac{R}{M}

and

C_{v}

are specific heats at constant pressure and constant volume respectively. It is observed that,

C_{p} - C_{v} = a

for hydrogen gas and

C_{p} - C_{v} = b

for nitrogen gas. The correct relation between

a

and

b

is:

EASY

Physics>Heat and Thermodynamics>Thermodynamics>Specific Heat Capacity

4.0 g

of a gas occupies

22.4

liters at NTP. The specific heat capacity of the gas at constant volume is

5.0 J K^{- 1} m o l^{- 1}

. If the speed of sound in this gas at NTP is

952 m s^{- 1}

, then the heat capacity at constant pressure is

(Take gas constant

R = 8.3 J K^{- 1} m o l^{- 1}

)

Important Questions on Thermodynamics

Learn and Prepare for any exam you want !