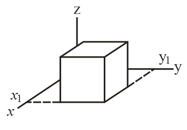
At each point on the surface of the cube shown in the figure, the electric field is parallel to the axis. The length of each edge of the cube is . On the top face of the cube the field of and on the bottom face it is . Determine the net charge contained within the cube.


Important Questions on Gauss' Law
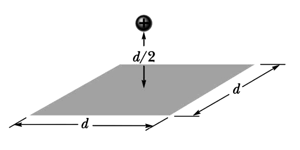
In the figure below, a proton is at a distance directly above the center of a square of side What is the magnitude of the electric flux through the square? (Think of the square as one of the faces of a cube with edge )
The figure shows cross sections through two large, parallel, nonconducting sheets with identical distributions of positive charge with surface charge density . In unit-vector notation, what is at points (a) above the sheets, (b) between them, and (c) below them?
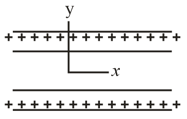
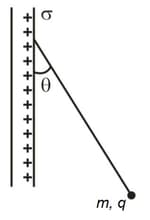
In the figure, a small, nonconducting ball of mass and charge (distributed uniformly through its volume) hangs from an insulating thread that makes an angle with a vertical, uniformly charged nonconducting sheet (shown in cross section). Considering the gravitational force on the ball and assuming the sheet extends far vertically and into and out of the page, calculate the surface charge density of the sheet.
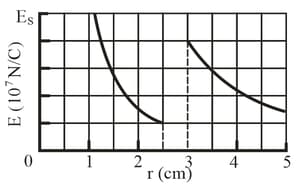
A charged particle is held at the center of a spherical shell. The figure gives the magnitude of the electric field versus radial distance . The scale of the vertical axis is set by . Approximately, what is the net charge on the shell?
The given figure shows a closed Gaussian surface in the shape of a cube of edge length , with one corner at , . The cube lies in a region where the electric field vector is given by with in meters. What is the net charge contained by the cube?