EASY
MHT-CET
IMPORTANT
Earn 100
Calculate the moment of inertia of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its moment of inertia about an axis passing through the centre and perpendicular to plane is .
(a)
(b)
(c)
(d)
100% studentsanswered this correctly

Important Questions on Rotational Motion
EASY
MHT-CET
IMPORTANT
EASY
MHT-CET
IMPORTANT
EASY
MHT-CET
IMPORTANT
EASY
MHT-CET
IMPORTANT
A solid sphere of radius has a moment of inertia about its geometrical axis. If it is melted into a disc of radius and thickness . If it's moment of inertia about the tangential axis (which is perpendicular to the plane of the disc), is also equal to , then the value of is equal to
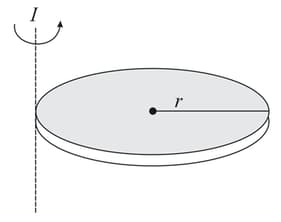
EASY
MHT-CET
IMPORTANT
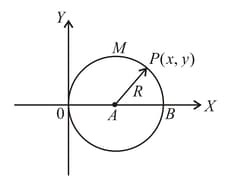
A disc of mass and radius is lying on the plane. The locus of all points on the plane about which the moment of inertia of the rod is same as that about will be,
EASY
MHT-CET
IMPORTANT
A thin uniform rectangular plate of mass is placed in plane as shown in the figure. The moment of inertia about -axis is and the moment of inertia about - axis is . The radius of gyration of the plate about the axis passing through and perpendicular to the plane of the plate is
EASY
MHT-CET
IMPORTANT
EASY
MHT-CET
IMPORTANT
