Calculate the moment of inertia of a uniform solid cone relative to its symmetry axis, if the mass of the cone is equal to m and the radius of its base to .

Important Questions on Rotational Mechanics
A uniform solid sphere is placed on a smooth horizontal surface. An impulse is given horizontally to the sphere at a height above the centre line. and are mass and radius of the sphere, respectively.
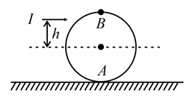
Find the angular velocity of the sphere and linear velocity of centre of mass of the sphere after impulse.
Find the minimum time after which the highest point will touch the ground,
Find the displacement of the centre of mass during this interval.
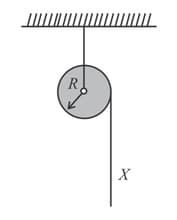
A uniform cylinder of radius and mass can rotate freely about a stationary horizontal axis . A thin cord of length and mass is wound on the cylinder in a single layer. Find the angular acceleration of the cylinder as a function of the length of the hanging part of the cord. The wound part of the cord is supposed to have its centre of gravity on the cylinder axis.
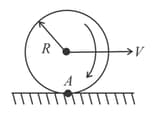
A point is located on the rim of a wheel of radius which rolls without slipping along a horizontal surface with velocity as shown in figure. Find:
(a) the modulus and the direction of the acceleration vector of the point ;
(b) the total distance s traversed by the point between the two successive moments at which it touches the surface.
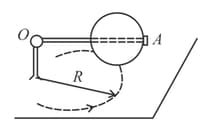
A uniform sphere of mass and radius rolls without sliding over a horizontal plane, rotating about a horizontal axle . In the process, the centre of the sphere moves with velocity along a circle of radius Find the kinetic energy of the sphere.
Consider a bicycle in vertical position accelerating forward without slipping on a straight horizontal road. The combined mass of the bicycle and the rider is and the magnitude of the accelerating torque applied on the rear wheel by the pedal and gear system is . The radius and the moment of inertia of each wheel is and (with respect to the axis) respectively. The acceleration due to gravity is .
(a) Draw the free diagram of the system (bicycle and rider ).
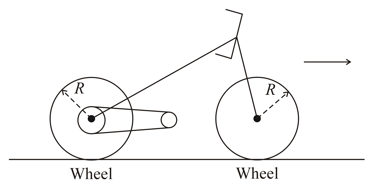
(b) Obtains the acceleration in terms of the above-mentioned quantities.
(c) For simplicity assume that the centre of mass of the system is at height from the ground and equidistant at from the centre of each of the wheels. Let be the coefficient of friction (both static and dynamic) between the wheels and the ground. Consider and no slipping. Obtain the conditions for the maximum acceleration of the bike.
(d) For calculate .
