Calculation the angular momentum about on the axis of rotation in following cases.
(i) 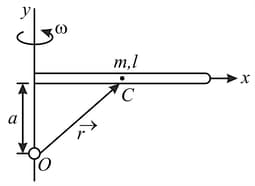 (ii)
(ii) 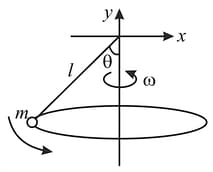
(i)
 (ii)
(ii) 

Important Questions on Rigid Body Dynamics: Part 2
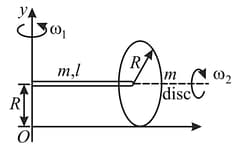
Calculation the angular momentum in following situation a disc is connected with a rod mass and length; The disc is free to rotate about its own axis. If whole system is rotating with and disk also rotate about its own axis with then calculation about origin.
A small block of mass is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius about the hole, with a tangential velocity of . The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is . What will be the radius of the circle when the cord breaks?
The device shown in figure rotates on the vertical axle as shown. The frame has negligible mass as compared to the four masses each of mass . Initial angular velocity of the system is . Due to an internal mechanism the spokes in the frame lengthen so that the radii of the masses become . Initially, it was . What will be the new angular velocity of the system?
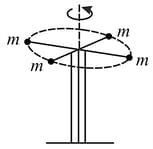
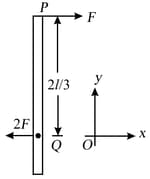
Find and of the smooth rod of mass and length .
A cylinder of mass and radius rolls on a stationary plank of mass . The lower surface of the plank is smooth and the upper surface is sufficiently rough with a coefficient of friction . A man is to hold the plank stationary with respect to the ground, as shown figure.
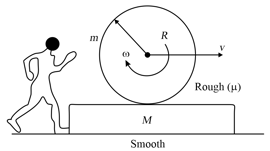
Find the force exerted by the man to keep the plank stationary.
