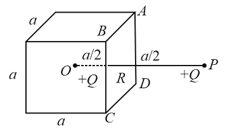
Consider a region in free space bounded by the surfaces of an imaginary cube having sides of length 'a' as shown in the diagram. A charge $+Q$ is placed at the centre $O$ of the cube. $P$ is such a point outside the cube that the line $OP$ perpendicularly intersects the surface $A B C D$ at $R$ and also $OR=RP=\frac{a}{2}$. A charge $+Q$ is placed at point $P$ also. What is the total electric flux through the five faces of the cube other than $ABCD$?

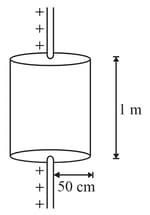
Electric charge is uniformly distributed along a long straight wire of radius $1 \mathrm{mm}$. The charge per length of the wire is $Q$ coulomb. Another cylindrical surface of radius $50 \mathrm{cm}$ and length $1 \mathrm{m}$ symmetrically encloses the wire as shown in the figure. The total electric flux passing through the cylindrical surface is 

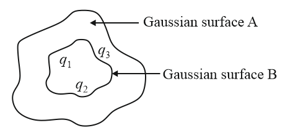
The electric flux for Gaussian surface $A$ that enclose the charged particles in free space is (given ${\mathrm{q}}_1=-14\mathrm{nC}, {\mathrm{q}}_2=78.85\mathrm{nC}, {\mathrm{q}}_3=-56\mathrm{nC})$ (Use:${\epsilon }_0=8.85\times {10}^{-12}{\text{ N}}^{-1} {\mathrm{m}}^{-2} {\mathrm{C}}^2$)

What is the nature of Gaussian surface involved in Gauss law of electrostatics? 

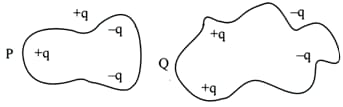
Arrangement of charges are shown in the figure. Flux linked with the closed surface $P \text{and} Q$, respectively are ______ and ___________

A charge $Q$ is enclosed by a Gaussian spherical surface of radius $R$. If the radius is doubled, then the outward electric flux will 

The total electric flux through a cube when a charge $8 q$ is placed at one corner of the cube is 

The inward and outward electric flux for a closed surface in units of ${\mathrm{Nm}}^2 {\mathrm{C}}^{-1}$ are respectively $8\times {10}^3$ and $4 \times 10^{3}$. Then the total charge inside the surface is [where, ${\epsilon }_0= \text{permittivity constant]}$

According to Gauss' theorem, electric field of an infinitely long straight wire is proportional to