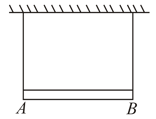
Consider a rigid body which consist of uniform hemispherical shell of radius $R$ and uniform cylindrical shell of height $L$ and radius $R$ (material of hemispherical shell and cylindrical shell are same). Find maximum value of $L$ so that complete rigid body remains in stable equilibrium in the position shown (neglect friction).

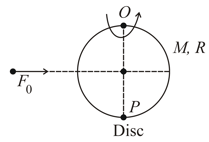
Horizontal force $F_0$ is applied on a uniform circular disc of mass $M$ and radius $R$ which can rotate in vertical $x-y$ plane about an axes passing through $O$ as shown. What is the acceleration of bottom most point $P$ on the disc at this instant?

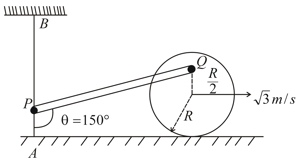
Consider the shown diagram. A fixed vertical smooth rod $AB$ is kept in front of a uniform disc of mass $m$ and radius $R$ which is rolling without slipping on a rough horizontal surface. Velocity of centre of disc is $\sqrt{3} \mathrm{m} {\mathrm{s}}^{-1}$. A rod $PQ$ of length $2 \mathrm{m}$ is connected with disc at $Q$, (point $Q$ is at a vertical distance of $\frac{R}{2}$ from centre of disc) by pin joint and other end of rod $PQ$ can freely slide over smooth vertical rod $AB$. At this instant rod $PQ$ makes an angle $\theta =150°$ with rod $AB$ as shown. Find the angular velocity of rod at this instant.

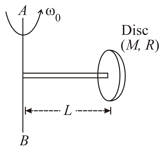
A uniform circular disc of mass $M\left(=1\mathrm{kg}\right)$ and radius $R\left(=1m\right)$ is fixed to vertical axis $AB$ with the help of a rod of length $L$ as shown. The disc rolls on a horizontal surface and is free to rotate about its centre. If there is no slipping at the point of contact of disc and horizontal surface then kinetic energy of the disc will be (given ${\omega }_0=2\mathrm{rad} {\mathrm{s}}^{-1}, L=1 \mathrm{m}$)

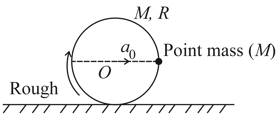
A uniform circular disc of mass $M$ and radius $R$ is having a point mass $M$ at its circumference is performing rolling without slipping over a rough horizontal surface as shown. Acceleration of point $O$ is $a_0$ towards right. If $N$ is the normal reaction on disc by the horizontal surface at this instant then

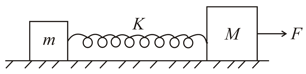
A block of mass $\mathrm{m}$ is connected to another block of mass $M$ by a massless spring of spring constant $K$. Blocks are kept on a smooth horizontal plane. Initially both the blocks are at rest and spring is unstressed. Force $F$ is applied on $M$ to right as shown in the figure then which of the following is correct?

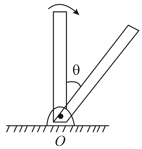
A rod of mass $\mathrm{m}$ and length $L$ is pivoted at the bottommost point $O$ and can freely rotate about the point $O$. The rod is disturbed from the vertical position so that it starts rotating about $O$. When it makes an angle $\theta$ with the vertical

A rod of mass $\mathrm{m}$ and length $L$ is pivoted at a  point $O$ and kept in horizontal position as shown in figure. Now it is released from this position so that it can rotate freely about the point $O$ in downward direction. When it becomes vertical

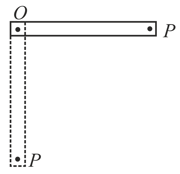
A horizontal rod of length $L$ is tied to two vertical strings symmetrically as shown in figure. One of the strings at point $B$ is cut at time $t=0$ and rod starts rotating about other end $A$ in downward direction. Then