Consider a spacecraft in an elliptical orbit around the earth. At the lowest point or perigee, of its orbit it is above the earth’s surface at the highest point or apogee, it is above the earth’s surface.
(a) What is the period of the spacecraft’s orbit ?
(b) Find the ratio of the spacecraft’s speed at perigee to its speed at apogee.
(c) Find the speed at perigee and the speed at apogee.
(d) It is desired to have the spacecraft escape from the earth completely. If the spacecraft’s rockets are fired at perigee, by how much would the speed have to be increased to achieve this? What if the rockets were fired at apogee ? Which point in the orbit is the most efficient to use? (Let the radius of earth is )

Important Questions on Gravitation
A satellite is put into a circular orbit with the intention that it hover over a certain spot on the earth’s surface. However, the satellite’s orbital radius is erroneously made too large for this to happen. At what rate and in what direction does the point directly below the satellite move across the earth’s surface?
What are:
(a) the speed and
(b) the period of a satellite in an approximately circular orbit above the surface of the earth? Suppose the satellite loses mechanical energy at the average rate of per orbital revolution. Adopting the reasonable approximation that due to atmospheric resistance force, the trajectory is a circle of slowly diminishing radius. Determine the satellite’s
(c) altitude (d) speed and (e) period at the end of its revolution. (f) Is angular momentum around the earth’s centre conserved for the satellite or the satellite-earth system.
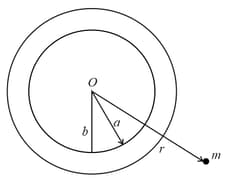
A sphere of density and radius has a concentric cavity of radius , as shown in the figure.
(a) Sketch the gravitational force exerted by the sphere on the particle of mass , located at a distance from the centre of the sphere as a function of r in the range
(b) Sketch the corresponding curve for the potential energy of the system.
(a) What is the escape speed for an object in the same orbit as that of earth around sun (take orbital radius ) but far from the earth? (Mass of the)
(b) If an object already has a speed equal to the earth’s orbital speed, what minimum additional speed must it be given to escape as in (a)?
A cosmic body moves towards the sun with velocity (when far from the sun) and aiming parameter , the direction of the vector relative to the centre of the sun as shown in the figure. Find the minimum distance by which this body will get to the sun (mass of sun)
Two stars of mass and are in circular orbits around their centre of mass. The star of mass has an orbit of radius , the star of mass has an orbit of radius. (Assume that their centre of mass is not accelerating and distance between stars is fixed)
(a) Show that the ratio of the orbital radii of the two stars equals the reciprocal of the ratio of their masses, that is
(b) Explain why the two stars have the same orbital period and show that the period,
