HARD

JEE Main/Advanced

IMPORTANT

Earn 100

Consider the following radioactive decay
${}^{90}X \overset{β - emission}{⟶} {}^{90}Y \overset{β - emission}{⟶} Z$
If half life of ${}^{90}Y$ is $73$ hours and that of ${}^{90}X$ is $20$ years, then the amount of ${}^{90}Y$ in equilibrium with $1 g$ of ${}^{90}X$ is

69.81% studentsanswered this correctly

Important Points to Remember in Chapter -1 - Chemical Kinetics and Nuclear Chemistry from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

1. Rate/velocity of Chemical Reaction:

$R a t e = \frac{Δ C}{Δ t} = \frac{\frac{m o l e}{l i t}}{s e c} = m o l e {l i t}^{- 1} {t i m e}^{- 1} = m o l e {d m}^{- 3} {t i m e}^{- 1}$ .

2. Types of Rates of Chemical Reaction:

For a reaction $R ⟶ P$

Average rate $= \frac{T o t a l c h a n g e i n c o n c e n t r a t i o n}{T o t a l t i m e t a k e n}$

$R_{i n s t a n t a n e o u s} = \underset{t \to 0}{l i m} [\frac{Δ c}{Δ t}] = \frac{d c}{d t} = - \frac{d [R]}{d t} = \frac{d [P]}{d t}$

3. Rate Law (dependence of rate on concentration of reactants):

Rate $= k {(c o n c .)}^{o r d e r} \to$ differential rate equation for rate expression.

Where $k =$ Rate constant $=$ specific reaction rate $=$ rate of reaction when concentration is unity.

$u n i t o f k = (c o n c)^{1 - o r d e r} {t i m e}^{- 1}$

4. Order of Reaction:

$m_{1} A + m_{2} B ⟶ p r o d u c t s .$

$R \propto [A]^{p} [B]^{q}$

Where $p$ may or may not be equal to $m_{1}$ & similarly q may or may not be equal to $m_{2}$ .

$p$ is order of reaction with respect to reactant $A$ and $q$ is order of reaction with respect to reactant $B$ and

$(p + q)$ is overall order of the reaction.

5. Molecularity of a Reaction:

It is defined as the number of molecules colliding with each other in an elementary reaction. For example: $A \to B$ reaction has molecularity $= 1$

For an elementary reaction, Molecularity $=$ Order.

For a complex reaction, Molecularity has no meaning. However, Molecularity of Rate determining step (RDS) can be approximately used to determine the overall rate of reaction.

6. Integrated Rate Laws:

$C_{0}$ or $' a^{'}$ is initial concentration and $C_{t}$ or $a - x$ is concentration at time $' t^{'}$

(i) For Zero Order Reaction:

$R a t e = k [c o n c .]^{0} = c o n s t a n t$

$R a t e = k = \frac{C_{0} - C_{t}}{t^{}} o r C_{t} = C_{0} - k t$

$U n i t o f k = m o l {l i t}^{- 1} {s e c}^{- 1},$ Time for completion $= \frac{C_{0}}{k}$

$a t t_{\frac{1}{2}}, C_{t} = \frac{C_{0}}{2}, s o k t_{\frac{1}{2}} = \frac{C_{0}}{2}$

$\Rightarrow t_{\frac{1}{2}} = \frac{C_{0}}{2 k} ∴ t_{\frac{1}{2}} \propto C_{0}$

(ii) For First Order Reaction:

Let $a 1^{s t}$ order reaction is $A ⟶$ Products.

$t = \frac{2.303}{k} \log \frac{a}{a - x} o r k = \frac{2.303}{t} \log \frac{C_{0}}{C_{t}}$

$⟹ t_{\frac{1}{2}} = \frac{l n 2}{k} = \frac{0.693}{k} =$ Independent of initial concentration.

$t_{A v g .} = \frac{1}{k} = 1.44 t_{\frac{1}{2}}$

Graphical representation:

$t = - \frac{2.303}{k} \log C_{t} + \frac{2.303}{k} \log C_{0}$

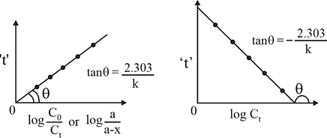
Question Image

(iii) Second Order Reaction:

2^nd order Reactions Two types

$A + A ⟶ p r o d u c t s$

$A a 0$

$(a - x) (a - x) x$

$∴ \frac{d x}{d t} = k (a - x)^{2}$

$\Rightarrow \frac{1}{(a - x)} - \frac{1}{a} = k t$

$A + B ⟶ p r o d u c t s .$

$a b 0$

$(a - x) (b - x) x$

$\frac{d x}{d t} = k (a - x) (b - x)$

$k = \frac{2.303}{(a - b)} \log \frac{b (a - x)}{a (b - x)}$

(iv) Pseudo first order reaction:

$∴ F o r A + B ⟶ P r o d u c t s [R a t e = K [A]^{1} [B]^{1}]$

$k = \frac{2.303}{t (a - b)} \log \frac{b (a - x)}{a (b - x)}$

Now if $' B^{'}$ is taken in large excess $b > > a$

$\Rightarrow k = \frac{2.303}{b t} \log \frac{a}{a - x}$

$' b^{'}$ is very large can be taken as constant.

$\Rightarrow k b = \frac{2.303}{t} l o g \frac{a}{a - x} \Rightarrow k^{'} = \frac{2.303}{t} \log \frac{a}{a - x}$

$k^{'} = k b$ is pseudo first order rate constant.

7. Methods to determine Order of a Reaction:

(i) Initial rate method:

$r = k [A]^{a} [B]^{b} [C]^{c}$

if $[b] =$ constant and $[c] =$ constant

then for two different initial concentrations of $A$ we have

$r_{0_{1}} = k {[A_{0}]}_{1}^{a}, r_{0_{2}} = k {[A_{0}]}_{2}^{a} \Rightarrow \frac{r_{0_{1}}}{r_{0_{2}}} = {(\frac{{[A_{0}]}_{1}}{{[A_{0}]}_{2}})}^{a}$

(ii) Using integrated rate law: It is a method of trial and error.

(iii) Method of half-lives:

For $n^{t h}$ order reaction $t_{\frac{1}{2}} \propto \frac{1}{{[R_{0}]}^{n - 1}}$

(iv) Ostwald Isolation Method:

rate $= k [A]^{a} [B]^{b} [C]^{c} = k_{0} [A]^{a}$

If B and C is taken in excess.

8. Methods to monitor the Progress of the First Order Reaction:

(i) Progress of gaseous reaction can be monitored by measuring total pressure at a fixed volume & temperature or by measuring total volume of mixture under constant pressure and temperature.

$A_{n} \overset{Δ}{\to} n A$

$∴ k = \frac{2.303}{t} l o g \frac{P_{0} (n - 1)}{n P_{0} - P_{t}}$ {Formula is not applicable when $n = 1$ , the value of n can be fractional also}.

Here, P_o and P_t represent the total pressure exerted by the system of gas at the starting of the reaction and at the reference time respectively.

(ii) By titration method:

$H_{2} O_{2} (l) \overset{}{\to} H_{2} O (l) + O_{2} (g)$

$a 0 0$

$a - x x \frac{x}{2}$

$∴ a \propto V_{0} a - x \propto V_{t}$

$\Rightarrow k = \frac{2.303}{t} \log \frac{V_{0}}{V_{t}}$

(iii) Study of acid hydrolysis of an ester:

$R C O O R^{'} (l) + H_{2} O (l) \overset{H^{+} (a q .)}{\to} R C O O H + R^{'} O H$

$V_{\infty} = V o l u m e o f N a O H u s e d a t t = \infty$ .

$V_{t} = V o l u m e o f N a O H u s e d a t r e f e r e n c e t i m e .$

$V_{o} = V o l u m e o f N a O H u s e d a t t = 0 .$

$k = \frac{2.303}{t} \log \frac{V_{\infty} - V_{0}}{V_{\infty} - V_{t}}$

(iv) By measuring optical rotation produced by the reaction mixture:

$R C O O R^{'} (l) + H_{2} O (l) \overset{H^{+} (a q .)}{\to} R C O O H + R^{'} O H$

$θ_{\infty} = O p t i c a l r o t a t i o n p r o d u c e d b y t h e m i x t u r e a t t i m e t = \infty .$ .

$θ_{0} = Optical rotation produced by the mixture at time t = 0 .$

$θ_{t} = O p t i c a l r o t a t i o n p r o d u c e d b y t h e m i x t u r e a t r e f e r e n c e t i m e .$

$k = \frac{2.303}{t} \log (\frac{θ_{0} - θ_{\infty}}{θ_{t} - θ_{\infty}})$

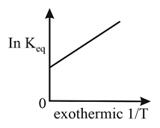
9. Effect of Temperature on Rate of Reaction:

$T . C . = \frac{K_{t} + 10}{K_{t}} = 2 t o 3$ (for most of the reactions)

Arrhenius theory of reaction rate:

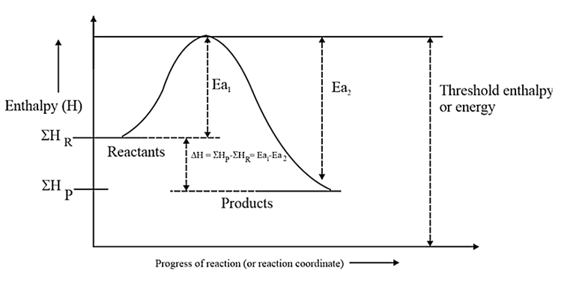
Question Image

${Σ H}_{R} =$ Summation of enthalpies of reactants.

${Σ H}_{P} =$ Summation of enthalpies of products.

$Δ H =$ Enthalpy change during the reaction.

$E_{a_{1}} =$ Energy of activation of the forward reaction.

$E_{a_{2}} =$ Energy of activation of the backward reaction.

${Σ H}_{P} > {Σ H}_{R} \to$ endothermic.

${Σ H}_{P} < {Σ H}_{R} \to$ exothermic.

$Δ H = ({Σ H}_{P} - {Σ H}_{R}) =$ enthalpy change:

$Δ H = {Σ H}_{P} - {Σ H}_{R}$

$E_{t h r e s h o l d} = E_{a_{1}} + {Σ H}_{R} = E_{a_{2}} + {Σ H}_{P}$

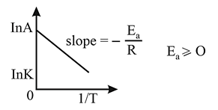
Arrhenius equation:

$k = A e^{- \frac{E_{a}}{R T}}$

$r = k [c o n c .]^{n}$

$\frac{d l n k}{d T} = \frac{E_{a}}{{R T}^{2}}$

$\log k = (- \frac{E a}{2.303 R}) \frac{1}{T} + \log A$

If $k_{1}$ and $k_{2}$ be the rate constant of a reaction at two different temperature $T_{1}$ and $T_{2}$ respectively, then we have:

$\log \frac{k_{2}}{k_{1}} = \frac{E_{a}}{2.303 R} (\frac{1}{T_{1}} - \frac{1}{T_{2}})$

$In k = \ln A - \frac{E_{a}}{R T}$

$T \to \infty, K \to A$

Question Image

10. Reversible Reactions:

$k_{f} = A_{f} e^{- \frac{E_{a}}{R T}}$

$k_{b} = A_{b} e^{- \frac{E_{b}}{R T}}$

$K_{e q} = \frac{k_{f}}{k_{b}} = (\frac{A_{f}}{A_{b}}) e^{- \frac{(E_{a} - E_{b})}{R T}}$

In $K_{e q} = - \frac{Δ H}{R T} + l n (\frac{A_{f}}{A_{b}})$

Question Image

Parallel $1^{s t}$ Order Reaction:

$\frac{[B]}{[C]} = \frac{k_{1}}{k_{2}} \Rightarrow E_{a} = \frac{E_{a_{1}} k_{1} + E_{a_{2}} k_{2}}{k_{1} + k_{2}}$ .

$x = \frac{k_{f} a}{k_{f} + k_{b}} (1 - e^{- (k_{f} + k_{b}) t})$

REVERSIBLE 1^ST ORDER REACTION: $A \overset{k_{f}}{\underset{k_{b}}{⇌}} B$

$k_{f} + k_{b} = \frac{1}{t} \ln (\frac{x_{e q .}}{x_{e q} - x})$

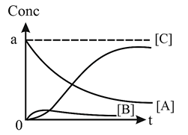
SEQUENTIAL $1^{S T}$ ORDER REACTION: $A \overset{k_{1}}{\to} B \overset{k_{2}}{\to} C$

${[A]}_{t} = {[A]}_{o} e^{- k_{1} t}$

${[B]}_{t} = \frac{k_{1} a}{k_{2} - k_{1}} \{e^{- k_{1} t} - e^{- k_{2} t}\} t_{B (m a x)} = \frac{1}{(k_{1} - k_{2})} \ln \frac{k_{1}}{k_{2}}$

$t_{B (m a x)} = T i m e t a k e n b y B t o r e a c h t h e m a x i m u m c o n c e n t r a t i o n .$

CASE-I:

$k_{1} ≫ k_{2}$

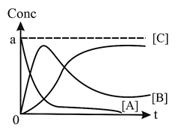
Question Image

CASE-II:

$k_{2} ≫ k_{1}$

Question Image

11. Introduction to Nuclear chemistry:

Nuclear chemistry is the study of the properties and reactions of atomic nuclei. In nuclear reaction only the nuclides (nuclide: the nucleus of a specific isotope) participates and overall (mass $+$ energy) remains conserved.

Radioactivity: The property of a nucleus emitting radiations like $α, β$ and $γ$ is known as radioactivity and the substance possessing the property is called a radioactive substance. The emission of these particle takes place because of the instability of the nucleus. Radioactivity is a property of nucleus.

12. Properties of $α, β$ -particles and $γ$ –rays:

Properties	Alpha	Beta	Gamma
Nature	Fast moving $H e$ nuclei $(H e^{2 +})$	Fast moving electrons	High energy electromagnetic
Representation	${}_{2}^{4}{H e}$ or $α$	${}_{- 1}^{0}e$ or ${}_{- 1}^{0}β$	$γ$ or ${}_{0}^{0}γ$
Charge	$2 u n i t (+ v e)$	$1 u n i t (- v e)$	No charge
Rest mass	$6.65 \times 10^{- 24} g {p a r t i c l e}^{- 1}$	$9.11 \times 10^{- 28} g {p a r t i c l e}^{- 1}$	$0$
Velocity	$\frac{1}{10}$ of light $(m i n .)$	nearly velocity of light	Same as light wave (max.)
Relative penetrating power	$1$	$\approx 100$	$\approx 10000$
Relative ionizing power	$\approx 10000$	$\approx 100$	$1$
Effect of electromagnetic field	Deflected toward $- v e$ electrode	Deflected toward $+ v e$ electrode	No effect
Kinetic energy	High	Low	-
Effect on $Z n S$ Screen	Maximum effect	Little effect	-

13. Types of Radioactive Decay:

(i) $α$ -decay causes decrease of atomic number of $2$ units and mass number by $4$ units.

Example: ${}_{84}^{215}P o \to {}_{82}^{211}P b + {}_{2}^{4}H e$

${}_{86}^{226}R a \to {}_{86}^{226}R n \to {}_{86}^{226}R n +_{2}^{4} H e$

All nuclides with atomic number greater than $82$ are beyond the band of stability and are radioactive.

(ii) $β$ -decay causes increase of atomic number by $1$ unit and no change in mass number.

Example: ${}_{88}^{228}R a \to_{89}^{228} A c +_{- 1}^{0} e$ ;

${}_{6}^{14}C \to_{7}^{14} N +_{- 1}^{1} e$

A neutron is converted to proton in this process.

${}_{0}^{1}n \to {}_{1}^{1}p +_{- 1}^{0} e$

Such emission occurs for the nuclei lying above the stability belt.

(iii) $γ$ -ray emission $(\begin{matrix} 0 \\ 0 \end{matrix} γ)$ causes no change in atomic number, since it represents the energy lost.

Example: ${}_{28}^{60}N i \to {}_{28}^{60}N i +_{0}^{0} γ$

(iv) Positron Emission: Causes decrease the atomic number by $1$ unit.

${}_{8}^{15}O \to_{7}^{15} N +_{+ 1}^{0} e$ ;

${}_{54}^{118}X e \to_{+ 1}^{0} e +_{53}^{118} I$

A proton is converted to neutron and positron in this process.

${}_{1}^{1}p \to_{0}^{1} n +_{+ 1}^{0} e$

Such emission occurs for the nuclei lying below the stability belt.

Position $({}_{+ 1}^{0}e)$ is a particle having the same mass as an electron, but positively charged.

(v) Electron-capture:

Causes decrease the atomic number by $1$ unit.

Example: ${}_{84}^{204}P o +_{- 1}^{0} e \to_{83}^{204} B i$ ;

${}_{19}^{40}K +_{- 1}^{0} e \to_{18}^{40} A r$

A proton is converted to neutron in this process.

${}_{1}^{1}p +_{- 1}^{0} e \to_{0}^{1} n$

Electron capture occurs with the nuclei lying below the stability belt, in which an electron from the $K$ -shell is captured by the nucleus.

14. Group Displacement Law:

In an $α$ -particle emission, the resulting element has a mass number less by four units and atomic number less by two units and so lies two places to the left in the periodic table.

In a $β$ -particle emission the resulting element has the same mass number but has an atomic number greater by one unit and so lies one place to the right in the periodic table.

15. Neutron/proton Ratio and Stability Zone:

(i) For atomic number $< 20$ , most stable nuclei have $n : p$ ratio nearly $1 : 1$ (except $H & A r$ ).

(ii) For $\frac{n}{p}$ ratio $> 1.5$ , nucleus is mostly unstable, Largest stable nucleus is ${}_{82}^{208}P b$ for which $\frac{n}{p}$ ratio is $1.53 .$

(iii) For atomic number $> 82$ , there are no stable nuclei.

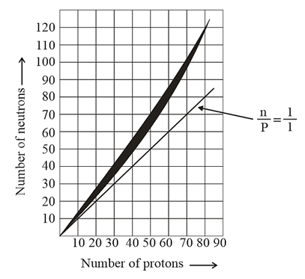
Question Image

Note: Heaviest stable nuclide is ${}_{82}^{208}P b$ , $t_{\frac{1}{2}}$ for ${}_{83}B i = 1.9 \times 10^{19} y e a r s$ which is $α$ -emitter reference.

16. Magic Numbers and Nuclear Stability:

Nuclei with $2, 8, 20, 28, 50, 82$ or $126$ protons or neutrons are unusually stable and have a larger number of stable isotopes than neighboring nuclei in the periodic table. These numbers are called magic numbers. They are supposed to represent completely filled nuclear shells of energy levels.

Nuclei with magic number of protons as well as neutrons have notably high stabilities. [Example: ${}_{2}^{4}H e,_{8}^{16} O,_{20}^{40} C a$ and ${}_{82}^{208}P b$ ]

17. Even Odd Theory:

Most naturally occurring nuclides have even numbers of neutrons and even numbers of protons. $165$ such stable nuclei are known. There exist $55$ known nuclei with even number of protons and odd number of neutrons, and $50$ known stable nuclei with odd number of protons and even number of neutrons. On the other hand, the number of known stable nuclei having odd numbers of both neutrons and protons is only $5$ .

18. Artificial Nuclear Reactions:

The first artificial transmutation was carried out by Rutherford in $1919$ who bombarded nitrogen gas with alpha particles and obtained hydrogen and oxygen.

$_{7}^{14} N +_{2}^{4} H e ⟶_{8}^{17} O +_{1}^{1} H$

(i) Alpha particle induced or $(α, n)$ type reactions:

$_{4}^{9} B e +_{2}^{4} H e ⟶_{6}^{12} C +_{0}^{1} n$

Since $α$ -particle is used and a neutron is produced, the reaction may be termed as $(α, n)$ reaction. In another $α$ -bombardment nuclear reaction, the isotope $({}_{15}^{30}P)$ produced is itself radioactive.

${}_{13}^{27}A l +_{2}^{4} H e \to_{15}^{30} P +_{0}^{1} n$

(ii) Deuteron-induced or $(D, α)$ type reaction:

${}_{8}^{16}O +_{1}^{2} H \to_{7}^{14} N +_{2}^{4} H e$

(iii) Proton-induced or $(p, γ)$ reaction

${}_{7}^{14}N +_{1}^{1} H \to {}_{8}^{15}O + γ$

(iv) Neutron-induced or $(n, γ)$ reaction

${}_{15}^{31}P + {}_{0}^{1}n \to {}_{15}^{32}P + γ$

19. Radioactive Decay:

(i) Radioactive decay is a first order process. The rate of nuclear decay is determined from measurements of the activity $(A)$ of a sample.

Hence $- \frac{d N}{d t} = λ N$ or $N = N_{0} e^{- λ t}$

where $N =$ number of radioactive nuclei at any time $t$ ; $N_{0} =$ number of radioactive nuclei at $t = 0$ ; $λ =$ decay constant.

S.I. units: The SI unit is becquerel $(B q)$ .

$1$ disintegration per second $(d p s) = 1 B q$

Other units: $1$ curie $(C i) = 3.7 \times 10^{10} d p s$ , $1$ Rutherford $(R d) = 10^{6} d p s$

(ii) Specific activity: Activity per unit mass of radioactive sample $(\frac{d p s}{g})$

(iii) Half life $(t_{\frac{1}{2}})$ : The time taken by half the nuclei (originally present) to decay.

$t_{\frac{1}{2}} = \frac{0.693}{λ}$

Note: After $n$ half-lives have passed, activity is reduced to $\frac{1}{2^{n}}$ of its initial value.

(iv) Average life $(t_{a v})$ : $t_{a v} = \frac{1}{λ} = 1.44 t_{\frac{1}{2}}$

20. Radioactive Equilibrium:

Among the members of a decay chain, the state which prevails when the ratios between the activities of successive members remain constant. (This is not an equilibrium in the strict sense since radioactive decay is an irreversible process).

21. Secular Equilibrium:

Radioactive equilibrium where the half life of the intermediate isotope is so long that the change first activity can be ignored during the period of interest and all activities remain constant.

$A \overset{λ_{A}}{\to} B \overset{λ_{B}}{\to} C$

Number of nuclei of $B$ is max. at $t_{m a x}$ ; $t_{m a x} = \frac{1}{(λ_{1} - λ_{2})} \ln (\frac{λ_{1}}{λ_{2}})$

$\frac{d N_{B}}{d t} = λ_{A} N_{A} - λ_{B} N_{B}$

Secular equilibrium occurs when $\frac{d N_{B}}{d t} = 0$ or $\frac{N_{B}}{N_{A}} = \frac{λ_{A}}{λ_{B}}$

22. Parallel Decay:

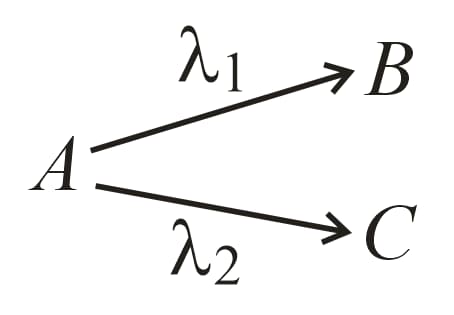
Question Image

$%$ of $B = (\frac{λ_{1}}{λ_{1} + λ_{2}}) \times 100$

$%$ of $C = (\frac{λ_{2}}{λ_{1} + λ_{2}}) \times 100$

23. Nuclear Fission:

In a nuclear fission reaction, a heavy nucleus splits up into two main fragments of lighter nuclei and several neutrons.

Of the three natural isotopes of uranium ${}_{92}^{238}U, {}_{92}^{235}U$ and ${}_{92}^{234}U$ the ${}_{92}^{235}U$ nucleus undergoes nuclear fission when bombarded with slow neutrons. The ${}_{92}^{236}U$ formed breaks up in several different ways, for example:

${}_{92}^{235}U +_{0}^{1} n \to_{92}^{236} U \to_{56}^{140} B a +_{36}^{93} K r + 3_{0}^{1} n$

${}_{92}^{235}U +_{0}^{1} n \to_{92}^{236} U \to_{54}^{144} X e +_{38}^{90} S r + 2_{0}^{1} n$

${}_{92}^{235}U +_{0}^{1} n \to_{92}^{236} U \to {}_{54}^{144}C s +_{37}^{90} R b + 2_{0}^{1} n$

(i) The key to the liberation of energy in the nuclear fission reaction is the production of two or more neutrons per reaction initiated by one neutron.

(ii) Atom bomb is based on nuclear fission.

24. General steps of a Nuclear Fission Chain Reaction:

(i) Initiation: The reaction of a single atom is needed to start the chain reaction Fission of ${}_{92}^{235}U$ is initiated by the absorption of a neutron.

(ii) Propagation: This part of the process repeats itself over and over, with each step yielding more product. The fission of ${}_{92}^{236}U$ releases neutrons that initiate the fission of other uranium atoms.

(iii) Termination: Eventually, the chain will end. Termination could occur if the reactant $({}_{92}^{235}U)$ is used up, or if the neutrons that continue the chain escape from the sample without being captured by ${}_{92}^{235}U$ .

25. Nuclear Fusion:

Just as the fission of heavy nuclei is accompanied by mass losses resulting into the liberation of large amounts of energy, the fusion of light nuclei is accompanied by mass losses and the evolution of large quantities of energy. Some such reactions and energy release in each process are shown below,

Fusion reaction	Mass loss	Energy released $(K J m o {l e}^{- 1})$
${}_{1}^{2}H +_{1}^{2} H \to_{2}^{4} H e$	$0.026$	$2.3 \times 10^{9}$
${}_{1}^{2}H +_{1}^{3} H \to_{2}^{4} H e +_{0}^{1} n$	$0.018$	$1.79 \times 10^{9}$

Compared with fission reactions, fusion reaction has advantage that large amounts of highly radioactive nuclides are not obtained as by-products which may pose problem of safe storage.

(i) Very high temperature is required for a fusion reaction.

(ii) Hydrogen bomb is based on nuclear fusion.

Einstein's mass-energy equation: Energy changes in nuclear reactions can determined by using Einstein's mass-energy equation $E = m c^{2}$ where $E$ is the energy equivalent of mass $m$ and $c$ is the velocity of light.

For a change of $1 a m u$ (atomic mass unit), the corresponding energy change, $E = 931 \times 10^{6} e V \approx 931 M e V$ , i.e., a mass of $1 a m u$ is equivalent to $931 M e V$ of energy.

26. Mass Defect:

It has invariably been found that the actual mass of an isotope of an element is less than the sum asses of the protons, neutrons and electron of the protons, neutrons and electrons present in it. This difference is called mass defect. it. The mass defect is nothing, but the loss of mass during the formation of the nucleus of the isotope.

(i) Mass defect in nuclear reaction:

$Δ m =$ mass of nuclei of reactants $-$ mass of nuclei of products.

Energy liberated in nuclear reaction: $Δ E = Δ m c^{2}$ .

(ii) Mass defect in an isotope formation:

Let $m_{p}, m_{n}$ and $m_{e}$ are the respective masses of proton, neutron, and electron. Then, the calculated mass of this isotope,

$M^{'} = Z m_{p} + Z m_{e} + (A - Z) m_{n} = Z m_{H} + (A - Z) m_{n}$

Let $M =$ Actual atomic mass as determined experimentally.

then, $Δ m =$ Mass defect $= M^{'} - M$

27. Binding Energy:

Loss of mass during the formation of the nucleus from nucleons is converted into energy. The release of energy imparts stability to the nucleus. The energy released when constituent nucleons combine to form a nucleus, is called binding energy of the nucleus. In other words, energy equal to binding energy will be needed to break up the nucleus into its constituent nucleons. Consequently, the greater the binding energy, the more stable is the nucleus.

28. Binding Energy and Nuclear Stability:

$B . E .$ per nucleon $= \frac{B . E .}{N o . o f n u c l e o n s}$

Binding energy per nucleon is a direct indicator of its nuclear stability. Higher the binding energy per nucleon of an isotope, greater is its nuclear stability.

Consider the following radioactive decay X90⟶β-emission Y90⟶β-emission Z If half life of Y90 is 73 hours and that of X90 is 20 years, then the amount of Y90 in equilibrium with 1 g of X90 is

Important Points to Remember in Chapter -1 - Chemical Kinetics and Nuclear Chemistry from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

Learn and Prepare for any exam you want !

Consider the following radioactive decay
${}^{90}X \overset{β - emission}{⟶} {}^{90}Y \overset{β - emission}{⟶} Z$
If half life of ${}^{90}Y$ is $73$ hours and that of ${}^{90}X$ is $20$ years, then the amount of ${}^{90}Y$ in equilibrium with $1 g$ of ${}^{90}X$ is