Consider two long straight line charges having linear charge densities ${\lambda }_1$ and ${\lambda }_2$. Derive expression for the force per unit length acting between them.

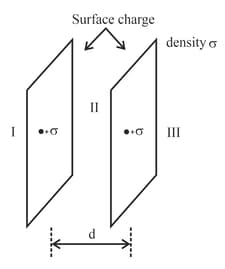
Let $\sigma$ be the uniform surface charge density of two infinite thin plane sheets shown in figure. Then the electric fields in three different region $E_I , E_{II}$ and $E_{III}$

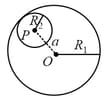
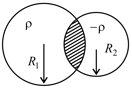
Two non-conducting spheres of radii $R_1$ and $R_2$ and carrying uniform volume charge densities $+\rho$ and $-\rho$, respectively, are placed such that they partially overlap, as shown in the figure. At all points in the overlapping region,

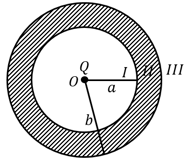
As shown in the figure, a point charge $Q$ is placed at the centre of conducting spherical shell of inner radius $a$ and outer radius $b$. The electric field due to charge $Q$ in three different regions $I, II \text{and} III$ is given by : $(I : r < a, II : a < r < b, III : r > b)$

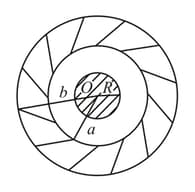
A solid metal sphere of radius $R$ having charge $q$ is enclosed inside the concentric spherical shell of inner radius $a$ and outer radius $b$ as shown in the figure. The approximate variation of electric field $\overrightarrow{E}$, as a function of distance $r$, from centre $O$, is given by:

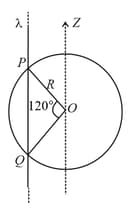
Using Gauss law, derive expression for electric field due to a spherical shell of uniform charge distribution $\sigma$ and radius $R$ at a point lying at a distance $x$ from the centre of shell, such that $0<x<R$.

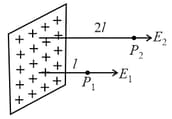
In the figure, a very large plane sheet of positive charge is shown. $P_1$ and $P_2$ are two points at distance $l$ and $2l$ from the charge distribution. If $\sigma$ is the surface charge density, then the magnitude of electric fields $E_1$ and $E_2$ at $P_1$ and $P_2$ respectively are