MEDIUM
Earn 100
Define L.P.P and its advantages.
Important Questions on Models
EASY
MEDIUM
For the data given in the table, the constraints are
| Diet | Diet | Minimum requirement | |
|
Proteins |
|||
|
Fats |
|||
| Vitamins |
EASY
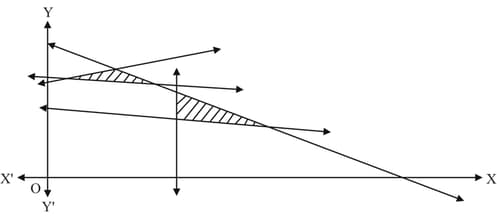
The feasible region for a given is as shown in the figure. The has
EASY
EASY
MEDIUM
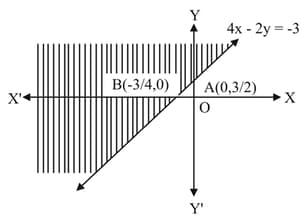
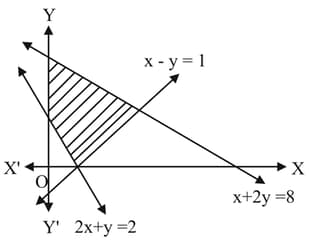
Find the linear inequations for which the shaded area in the following figure is the solution set:
EASY
EASY
For the data given in table, the constraints are
| Maximum availability | |||
| Number of labours | |||
| Work hours |
EASY
EASY
EASY
MEDIUM
EASY
EASY
EASY
EASY