Derive an expression for the angular frequency of small oscillation of the bob of a simple pendulum when it is immersed in a liquid of density $\sigma .$ Assume the density of the bob as $\rho$ and length of the string as $l.$

An $L$-shaped bar of mass $M$ is pivoted at one of its end so that it can freely rotate in a vertical plane, as shown in the figure.

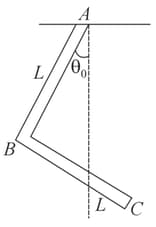
Find the value of ${\theta }_0$ at equilibrium.

An $L$-shaped bar of mass $M$ is pivoted at one of its end so that it can freely rotate in a vertical plane, as shown in the figure.

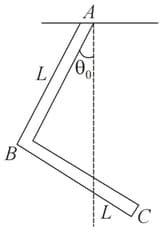
If it is slightly displaced from its equilibrium position, find the frequency of oscillation.

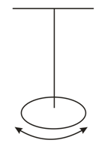
A uniform disc of radius $5.0 \mathrm{cm}$ and mass $200 \mathrm{g}$ is fixed at its centre to a metal wire, the other end of which is fixed to a ceiling. The hanging disc is rotated about the wire through an angle and is released. If the disc makes torsional oscillations with time period $0.20 \mathrm{s},$ find the torsional constant of the wire.

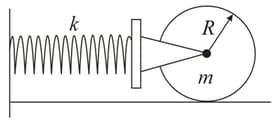
A solid cylinder is attached to a massless spring so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by the cylinder if $m=$ mass of cylinder and $k=$ spring constant.

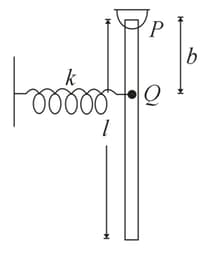
A uniform rod of mass $m$ and length $l$ hangs from a rigid support (smooth pivot) $P.$ A light spring of stiffness $k$ is rigidly attached with the rod at a point $Q$ at a distance $b$ below the pivot. Find the angular frequency of oscillation of the rod.

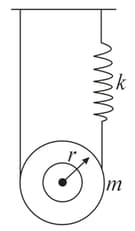
The pulley shown in figure has a radius $r,$ moment of inertia $I$ about its axis and mass $m.$ Find the time period of vertica oscillations of its center of mass. The spring constant of spring is $K$ and the spring does not slip over the pulley.

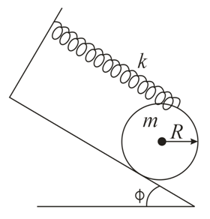
A uniform cylinder of mass $m$ and radius $R$ is in equilibrium on an inclined plane by the action of a light spring of stiffness $k,$ gravity and reaction force acting on it. If the angle of inclination of the plane is $\varphi ,$ find the angular frequency of small oscillation of the cylinder.