Derive an expression for the gravitational field due to a uniform rod of length and mass at a point on its perpendicular bisector at a distance from the centre.

Important Questions on Gravitation
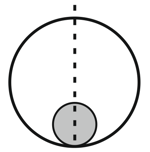
A solid sphere of mass and radius is placed inside a hollow thin spherical shell of mass and radius as shown. A particle of mass is placed on the line joining the two centres at a distance from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
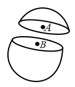
A uniform metal sphere of radius and mass is surrounded by a thin uniform spherical shell of equal mass and radius . The centre of the shell falls on the surface of the inner sphere. Find the gravitational field at points and shown in the figure.
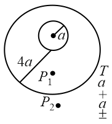
A thin spherical shell having uniform density is cut in two parts by a plane and kept separated as shown in figure. is the centre of the plane section of the first part and is the centre of the plane section of the second part.
Show that the gravitational field at due to the first part is equal in magnitude to the gravitational field at due to the second part.