Derive expressions for linear velocity at lowest point, midway and top position for a particle revolving in a vertical circle if it has to just complete circular motion without string slackening at top.
Important Questions on Rotational Dynamics
(Take the radius of the drum to be 1.25 m and its axle to be horizontal) :
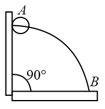
A small block slides down from the top of hemisphere of radius as shown in the figure. The height at which the block will lose contact with the surface of the sphere is . (Assume there is no friction between the block and the hemisphere)
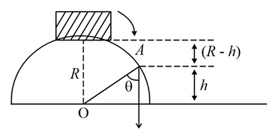
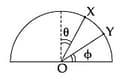
A particle is released on a vertical smooth semicircular track from point so that, makes angle from the vertical (see figure). The normal reaction of the track on the particle vanishes at the point where makes an angle with the horizontal. Then
A ball is released from rest from point of a smooth semi-spherical vessel as shown in figure. The ratio of the centripetal force and normal reaction on the ball at point is while angular position of point is with respect to point . Which of the following graphs represent the correct relation between and when ball goes from to ?
A particle of mass m performs vertical motion in a circle of radius r. Its potential energy at the highest point is ____.
(g is the acceleration due to gravity)
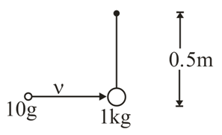
A bullet of , moving with velocity , collides head-on with the stationary bob of a pendulum and recoils with velocity . The length of the pendulum is and mass of the bob is . The minimum value of , so that the pendulum describes a circle. (Assume the string to be inextensible and )
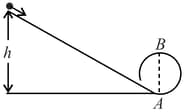
A body initially at rest and sliding along a frictionless track from a height (as shown in the figure) just completes a vertical circle of diameter . The height is equal to,