HARD
MYP:4-5
IMPORTANT
Earn 100
Describe how to transform the graph of to .

Important Questions on Trigonometric Functions
HARD
MYP:4-5
IMPORTANT
Describe how to transform the graph of to .
HARD
MYP:4-5
IMPORTANT
Describe how to transform the graph of to .
HARD
MYP:4-5
IMPORTANT
Describe how to transform the graph of to .
HARD
MYP:4-5
IMPORTANT
Describe how to transform the graph of to .
HARD
MYP:4-5
IMPORTANT
Describe how to transform the graph of to .
HARD
MYP:4-5
IMPORTANT
Describe how to transform the graph of to .
HARD
MYP:4-5
IMPORTANT
Describe how to transform the graph of to .
HARD
MYP:4-5
IMPORTANT
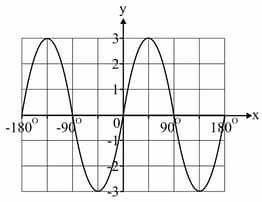
The graph given below is a transformation of either or . Identify the transformation(s) on the graph and write the function that describes the graph.