Determine the radius of an incircle by drawing an inscribing circle of a regular hexagon of side .
Important Questions on Constructions
Use ruler and compass only for answering the question.
Draw a circle of radius . Mark the centre as . Mark a point outside the circle at a distance of from the centre. Construct two tangents to the circle from the external point .
Measure and write down the length of any one tangent.
Which of the following steps is INCORRECT to construct a circle of the radius with centre and then drawing two tangents to the circle from where is a point outside the circle such that
Steps of construction
Step : Draw a circle with as center and radius
Step : Mark a point outside the circle such that
Step : Join and bisect it at .
Step : Draw a circle with as centre and radius equal to to intersect the given circle at the points and ’.
Step : Joint and . Then, and are the required tangents.
Given, a with and with incircle in the figure below:
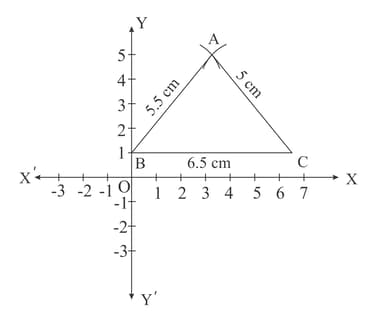
The distance from centre of the circle to vertex of is
Arrange the following steps of construction while constructing a pair of tangents to a circle, which are inclined to each other at an angle of to a circle of radius
Steps of Construction
Step : Draw any diameter of this circle.
Step : Draw and . Let and intersect each other at . Then and are the desired tangents to the given circle, inclined at an angle of
Step : Draw a circle with as Centre and radius .
Step : Construct such that radius meets the circle at
Steps of Construction
Step . Take a point on the plane paper and draw a circle of radius . Also, draw a concentric circle of radius .
Step : Find the mid-point of and draw a circle of radius , Suppose this circle intersects the circle of radius at and
Step : Join and to get the desired tangents.
The construction steps to draw a pair of tangents to the circle of radius from a point away from its centre, are given below but not in correct order, select the correct order from the options below.
A pair of tangents to the given circle can be constructed as follows.
Step 1: Taking M as centre and MO as radius, draw a circle.
Step 2: Let this circle intersect the previous circle at point Q and R.
Step 3: Taking any point O of the given plane as centre, draw a circle of radius. Locate a point P, away from O. Join OP.
Step 4: Bisect OP. Let M be the mid-point of PO.
Step 5: Join PQ and PR. PQ and PR are the required tangents.
Arrange the following steps of construction while constructing a pair of tangents to a circle of radius from a point away from the center of the circle.
Steps of Construction
Step : Bisect the line segment and let the point of bisection be
Step : Taking as centre and as radius, draw a circle. Let it intersect the given circle at the point and
Step : Draw a circle of radius
Step : Join and
Step : Take an external point which is away from its centre. Join
Steps of Construction
Step : Draw a circle of radius and take a point outside the circle and draw a secant intersecting the circle at and .
Step : Produce to such that . Draw a semicircle with as diameter.
Step : Draw , intersecting the semicircle at . With as Centre and as radius draw arcs to intersect the given circle at and ’.
Step : Join and . Then, and ’ are the required tangents.
Draw a circle of radius . From a point away from its centre, construct the pair of tangents to the circle. Below given are the steps for construction. Arrange them in order
A. Taking as centre and as radius draw a circle
B. Join and
C. Taking any point as centre draw a circle of radius-locate a point P, away from
D. Bisect and let be the midpoint of
E. The circle interests the previous circle at points and
Which of the following steps is INCORRECT to construct a tangent to the circle of radius at the point on it without using the center of the circle.
Steps of Construction
Step : Draw a circle of radius .
Step : Mark a point on it.
Step : Draw any chord
Step : Take a point in the minor arc
Step : Join and
Step : Make .
Step : Produce to . Then, is the required tangent at .
Given, a with and with incircle in the figure below:
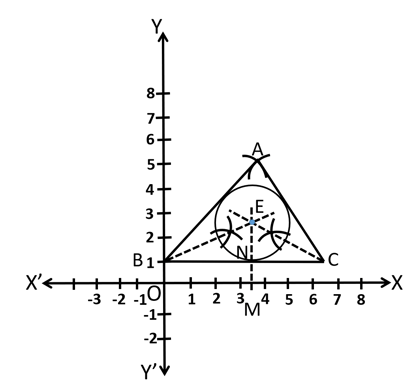
The radius of incircle is
Steps of Construction
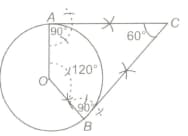
Step . With Centre and radius , draw a circle.
Step . Taking a point on the circle and draw
Step . Draw a perpendicular on at Draw another perpendicular on at .
Step . Let the two perpendiculars meet at Thus and are the two required tangents to the given circle which are inclined to each other at
Which of the following steps of construction is INCORRECT while drawing a tangent to a circle of radius and making an angle of with a line passing through the center.
Steps of Construction
Step : Draw a circle with Centre and radius .
Step : Draw a radius of this circle and produce it to .
Step : Construct an angle equal to the complement of i.e. equal to
Step : Draw a perpendicular to at which intersects produced at
Clearly, is the desired tangent such that .
Given, a with and with incircle in the figure below.
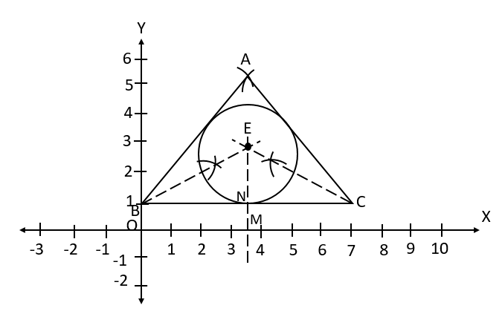
The distance from the centre of the circle to vertex of is _____ units rounded off to two decimal places.
Let be a right triangle in which and is the perpendicular from on . The circle through is drawn. Given below are the steps of constructions of a pair of tangents from to this circle. Which of the following steps is INCORRECT?
Steps of Construction
Step : Draw and perpendicular from on .
Step : Draw a circle with as a diameter. This circle will pass through
Step : Let be the mid-point of . Join
Step : Draw a circle with as diameter. This circle cuts the circle drawn in step at and and are desired tangents drawn from to the circle passing through and
Arrange the steps of construction while constructing a pair of tangents to a circle of radius from a point away from its Centre.
Steps of Construction
Step : Join and bisect it. Let is the mid-point of .
Step : Join and . and are the required tangents. Length of tangents
Step : With as centre, draw a circle of radius
Step : Taking as centre and as radius, draw a circle intersecting the given circle at the points and
Step : Take a point at a distance of from .

