EASY
Earn 100

Draw a diagram of standing wave formed inside the organ pipe with both ends closed for first harmonic.

Important Questions on Waves

EASY
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
A closed organ pipe and an open organ pipe have their first overtones identical in frequency. Their lengths are in the ratio
MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
A stationary tuning fork is in resonance with an air column in a pipe. If the tuning fork is moved with a speed of 2 m s-1 in front of the open end of the pipe and parallel to it, the length of the pipe should be changed for the resonance to occur with the moving tuning fork. If the speed of sound in air is 320 m s-1, the smallest value of the percentage change required in the length of the pipe is ________.
MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
A pipe open at one end has length 0.8 m. At the open end of the tube a string 0.5 m long is vibrating in its 1st overtone and resonates with fundamental frequency of pipe. If tension in the string is 50 N, the mass of string is (speed of sound =320 m s-1)
MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes

A closed organ pipe of length L and an open organ pipe contain gases of densities ρ1 and ρ2 respectively. The compressibility of gases are equal in both the pipes. Both the pipes are vibrating in their first overtone with same frequency. The length of the open pipe is x3Lρ1ρ2, where x is _______.  

(Round off to the Nearest Integer)

EASY
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
The fundamental frequency of an air column in a pipe closed at one end is 100 Hz. If the same pipe is open at both the ends, the frequencies produced in Hz are
EASY
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
First overtone frequency of a closed organ pipe of length L1 is equal to the 2nd  harmonic frequency of an open organ pipe of length L2. Then the ratio L1L2=?
MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
On closing an open organ pipe from one end, it is noticed that the frequency of third harmonic is 50 Hz more than the fundamental frequency of vibration in open organ pipe. The fundamental frequency of open organ pipe is
HARD
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes

How are stationary waves formed in closed pipes? Explain various modes of vibrations and obtain relations for their frequencies.

A closed organ pipe 70 cm long is sounded. If the velocity of sound is 331 m sec-1, what is the fundamental frequency of vibrations of the air column?

MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
A pipe of 1 m length is closed at one end. Taking the speed of sound in air as 320 m s-1, the air column in the pipe cannot resonate for the frequency in Hz
HARD
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
A pipe of length 85 cm is closed from one end. Find the number of possible natural oscillations of air column in the pipe whose frequencies lie below 1250 Hz. The velocity of sound in air is 340 m/s.
MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
A tuning fork is vibrating at 250 Hz. The length of the shortest closed organ pipe that will resonate with the tuning fork will be _____cm. (Take speed of sound in air as 340 m s-1 )
EASY
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
The fundamental frequency of a closed organ pipe of length 20 cm is equal to the second overtone of an organ pipe open at both the ends. The length of the organ pipe open at both the ends is
HARD
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
Show that even as well as odd harmonics are present as overtones in the case of an air column vibrating in a pipe open at both the ends.
MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
A cylindrical tube open at both ends has a fundamental frequency f in air. The tube is dipped vertically in water so that 60 % of the tube is in water. Then the fundamental frequency of air column is
HARD
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
Show that all harmonics are present in case of an air column vibrating in a pipe open at both ends.
MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
The first overtone frequency of an open organ pipe is equal to the fundamental frequency of a closed organ pipe. If the length of the closed organ pipe is 20 cm. The length of the open organ pipe is _____ cm
EASY
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes

A tuning fork is used to set up a wave in a pipe of length L closed at one end (see figure).

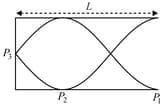
Question Image

Then,

MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
The number of possible natural oscillations of air column in a pipe closed at one end of length 85 cm whose frequencies lies below 1250 Hz are: (velocity of sound =340 ms-1)
HARD
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
The end correction of a resonance column is 1 cm. If the shortest length resonating with the tuning fork is 10 cm, the next resonating length should be
MEDIUM
Physics>Waves and Thermodynamics>Waves>Standing Waves in Pipes
A closed organ pipe has a fundamental frequency of 1.5 kHz. The number of overtones that can be distinctly heard by a person with this organ pipe will be (Assume that the highest frequency a person can hear is 20,000 Hz).