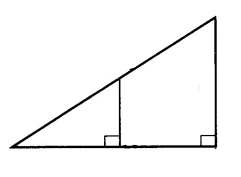
Draw a right triangle and the perpendicular from the midpoint of the hypotenuse to the base. Prove that this perpendicular is half the perpendicular side of the larger triangle.

Draw a right triangle. Prove that the perpendicular drawn from the midpoint of the hypotenuse to the base bisects the base of the triangle.

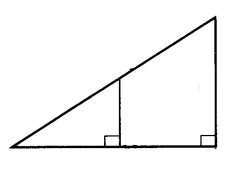
Draw a right triangle and the perpendicular from the midpoint of the hypotenuse to the base. Prove that in the larger triangle the distances from the midpoint of the hypotenuse to all the vertices are equal.

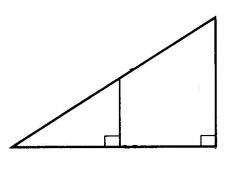
Draw a right triangle and the perpendicular from the midpoint of the hypotenuse to the base.  Prove that the circumcentre of a right triangle is the midpoint of its hypotenuse.

In the parallelogram $ABCD$, the line drawn through a point $P$ on $AB$, parallel to $BC$, meets $AC$ at $Q$. The line through $Q$, parallel to $AB$ meets $AD$ at $R$. 

Prove that $\frac{AP}{PB}=\frac{AR}{RD}$

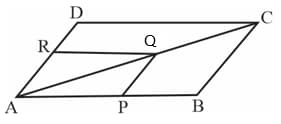
In the picture below, two vertices of a parallelogram are joined to the midpoints of two sides. Prove that these lines divide the diagonal in the picture into three equal parts.

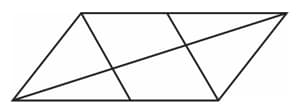
Prove that the quadrilateral formed by joining the midpoints of a quadrilateral is a parallelogram. What if the original quadrilateral is a rectangle? What if it is a rhombus?