Draw rough diagrams to illustrate the open curve.

(i) A Point is a mark of position. It occupies a position, and its location can be ascertained.

(ii) Line is straight and extends indefinitely in both directions.

(iii) An unlimited number of lines can be drawn through a given point.

(iv) Exactly one line passes through two different given points in a plane and it lies wholly in that plane.

(v) Three or more points are collinear if all of them lie on the same line.

(vi) Three or more lines are concurrent if all of them pass through the same point which is called their point of concurrence.

2. Plane:

(i) Plane is a flat smooth surface which extends indefinitely in all directions.

(ii) Two lines in a plane either intersect at exactly one point or are parallel.

(iii) Two planes either intersect or are parallel. If they intersect, they intersect in a line.

3. Line Segment:

(i) A line segment is a portion of a line. If $\mathrm{A}$ and $\mathrm{B}$ are two points in a plane, the part $\mathrm{AB}$ of the line through $\mathrm{A}$ and $\mathrm{B}$ is called a line segment $\mathrm{AB}$. The points $\mathrm{A}$ and $\mathrm{B}$ are called the endpoints of this segment.

(ii) A line segment has two endpoints, and a line has no end points.

(iii) There is a unique line segment joining two given points $A$ and $B$.

(iv) The line segment $AB$ is the same as the line segment $BA$.

4. Curves:

(i) If we take a piece of paper and it is just doodled. Then the pictures obtained because of doodling are called Curves.

(ii) A Curve which does not cut itself is called an Open Curve and a Curve which cuts itself is called a Closed Curve.

5. Polygon:

(i) A Polygon is a closed curve formed by the line segments such that:

(a) no two-line segments intersect except at their endpoints.

(b) no two-line segments with a common endpoint are coincident.

(ii) The Line segments forming a Polygon are known as its sides and their endpoints are known as the vertices of the Polygon.

(iii) Any two sides of a Polygon with a common endpoint are called the adjacent sides of the Polygon.

(iv) The endpoints of the same side of a Polygon are known as the adjacent vertices.

(v) The line segments joining the non-adjacent vertices are called the diagonals of the Polygon.

(vi) A Polygon is a Convex Polygon if the line segment joining any two points inside it lies completely inside the Polygon.

6. Angles:

(i) An angle is a figure formed by two rays with the same initial point. The initial point is called the vertex and the two rays are called the arms of the angle.

(ii) The amount of rotation through which one of the arms of a given angle must be rotated about its vertex to bring it to the position of the other, is called the magnitude of the angle.

(iii) The standard unit of measurement of an angle is Degree.

(iv) $1$ right angle $=90°, 1°=60\text{'}, 1\text{'}=60"$

(v) Two or more angles having the same magnitude are said to be equal.

7. Types of Angles:

(i) A complete turn of a ray $\mathrm{OA}$ about $\mathrm{O}$ describes a complete angle.

(ii) A half turn of a ray OA about O describes a straight angle, $1$ straight angle $=2$ right angles $=180°$.

(iii) A quarter turn of a ray $OA$ about $O$ describes a right angle,$1$ right angle $=90°$.

(iv) Zero angle $=0°, 0°<$ Acute angle $<90°, 90°<$ Obtuse angle $<180°$.

8. Triangle:

(i) A triangle is a figure made up by three-line segments joining, in pairs, three non-collinear points. That is, if $\mathrm{A}, \mathrm{B}, \mathrm{C}$ are three non-collinear points, the figure formed by three-line segments $AB, BC \mathrm{and} CA$ is called a triangle with vertices $A, B, C$.

(ii) The three-line segments forming a triangle are called the sides of the triangle.

(iii) The three sides and three angles of a triangle are together called the six parts or elements of the triangle.

(iv) The interior of a triangle is made up of all such points $P$ of the plane, as are enclosed by the triangle.

(v) The exterior of a triangle is that part of the plane which consists of those points $Q$, which are neither on the triangle nor in its interior.

(vi) The interior of a triangle together with the triangle itself is called the Triangular region.

9. Types of Triangle:

(i) A triangle whose two sides are equal, is called an Isosceles Triangle.

(ii) A triangle whose all sides are equal, is called an Equilateral Triangle.

(iii) A triangle whose no two sides are equal, is called a Scalene Triangle.

(iv) A triangle whose all the angles are acute is called an Acute Triangle.

(v) A triangle whose one of the angles is a right angle is called a Right Triangle.

(vi) A triangle whose one of the angles is an obtuse angle is called an Obtuse Triangle.

10. Quadrilateral:

(i) A figure formed by four points $A, B, C \mathrm{and} D$ in a plane such that no three of them are collinear and the line segments $AB, BC, CD \mathrm{and} DA$ do not intersect except at their end points is called a Quadrilateral.

(ii) Line segments $AB, BC, CD \mathrm{and} DA$ are called its sides and the line segments $AC \mathrm{and} BD$ are called diagonals.

(iii) $AB, CD \mathrm{and} AD, BC$ are two pairs of opposite sides.

(iv) Two sides of a Quadrilateral are called its adjacent sides if they have a common end point.

(v) Angles having a common side as an arm are called Adjacent Angles. Non-adjacent angles are called Opposite angles.

(vi) The interior of a Quadrilateral $ABCD$ together with quadrilateral $ABCD$ is called the Quadrilateral region.

11. Types of Quadrilateral:

(i) A Quadrilateral having exactly one pair of parallel sides is called a Trapezium.

(ii) A Quadrilateral is a Parallelogram if its both pairs of opposite sides are parallel.

(iii) A Parallelogram having all sides equal is called a Rhombus.

(iv) A Parallelogram whose each angle is a right angle is called a Rectangle.

(v) A Rectangle with a pair of adjacent sides equal is called a Square.

(vi) A Quadrilateral having two pairs of equal adjacent sides and unequal opposite sides is called a Kite.

12. Circle:

(i) A Circle with centre $O$ and radius $r$ is the figure consisting of all those points of a plane through $O$, which are at a constant distance $r$ from $O$.

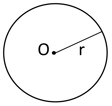
(ii) A Line segment with one-end at the centre of a circle, and the other on the circle is called a Radius of the Circle.

(iii) A Line segment passing through the centre of a circle, and having its endpoints on the circle, is called a Diameter of the Circle.

(iv) All radii of a Circle are equal.

(v) Diameter $=2\times ($Radius$)$.

(vi) All the diameters of a Circle are equal.

(vii) The diameters of a Circle are concurrent. The Centre is the point common to all diameters.

(viii) A point lies in the ‘Interior of a Circle’, On the Circle, or in the Exterior of the Circle, according as its distance from the centre is less than, equal to or greater than the Radius of the Circle, respectively.

(ix) The Interior of a circle together with the circle itself is called the Circular Region.

13. Terms Related to Circle:

(i) A line segment with its endpoints lying on a Circle is called a Chord of the Circle.

(ii) Diameter is the longest Chord of the Circle.

(ii) The endpoints of a diameter of a Circle divide the Circle into two parts; each part is called a semi-circle.

(iii) A diameter of a Circle divides the circular region into two parts; each part is called a semicircular region.

(iv) The perimeter of a Circle is called its Circumference.

(v) Two points of a Circle divide the Circle into two parts; each part is called an Arc of the Circle.

(vi) A chord of a circle divides the circular region into two parts; each part is called a segment of the circle.

(vii) The segment containing the centre of the circle is called the major segment and other part is called the minor segment of the circle.

(viii) A line passing through a Circle and intersecting the circle at two points is called a Secant of the circle.

14. Lines and Transversal:

(i) A line which intersects two or more given lines at distinct points is called a Transversal to the given line.

(ii) Lines in a plane are parallel if they do not intersect when produced indefinitely in either direction.

(iii) The distance between two intersecting lines is zero.

(iv) The distance between two parallel lines is the same everywhere and is equal to the perpendicular distance between them.

(v) If two parallel lines are intersected by a transversal, then,

(a) pairs of alternate (interior or exterior) angles are equal,

(b) pairs of corresponding angles are equal,

(c) interior angles on the same side of the transversal are supplementary.

(vi) If two lines are intersected by a transversal, then they are parallel if any are of the following is true:

(a) the angles of a pair of corresponding angles are equal, or 

(b) the angles of a pair of alternate interior angles are equal, or

(c) the angles of a pair of interior angles on the same side of the transversal are supplementary.