Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.

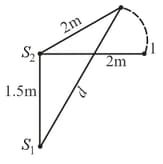
Two coherent sources of sound, $S_1$ and $S_2,$ produce sound waves of the same wavelength $\lambda =1 \mathrm{m}$ are in phase. $S_1$ and $S_2$ are placed $1.5 \mathrm{m}$ apart (see fig). A listener, located at $\mathrm{L}$, directly in front of $S_2$, finds that the intensity is at a minimum when he is $2 \mathrm{m}$ away from $S_2$. The listener moves away from $S_1$, keeping the distance from $S_2$ fixed. The adjacent maximum of intensity is observed when the listener is at a distance $d$ from $S_1$. Then $d$ is :

The Young's double slit experiment is performed with blue light and green light of wavelengths $4360 \mathrm{\AA }$ and $5460 \mathrm{\AA }$ respectively. If $X$ is the distance of $4^{th}$ maxima from the central one, then

Two coherent point sources $S_1$ and $S_2$ are separated by a small distance $d$ as shown in the figure. The fringes obtained on the screen will be

In a Young's double slit experiment with light of wavelength $\mathrm{\lambda ,}$ the separation of slits is $d$ and distance of screen is $D$ such that $D\gg d\gg \lambda$ . If the Fringe width is $\beta$ , the distance from point of maximum intensity to the point where intensity falls to half of the maximum intensity on either side is: