Earth can be thought of as a sphere of radius . Any object (or a person) is performing circular motion around the axis of the earth due to earth's rotation (period day). What is the acceleration of object on the surface of earth (at equator) towards its centre? What is it at latitude ? How does these accelerations compare with ?

Important Questions on Motion in a Plane
| column I | column II |
| (a) | (i)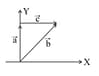 |
| (b) | (ii)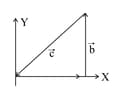 |
| (c) | (iii)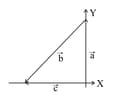 |
| (d) | (iv)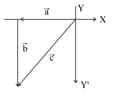 |
If and then match the relations in column I with the angle between and is column II.
| column I | column II |
| (a) | (I) |
| (b) | (ii) |
| (c) | (iii) |
| (d) | (iv) |
A hill is high. Supplies are to be sent across the hill using a canon that can hurl packets at a speed of over the hill. The canon is located at a distance of from the foot of the hill and can be moved on the ground at a speed of ; so that its distance from the hill can be adjusted. What is the shortest time in which a packet can reach on the ground across the hill? Take .
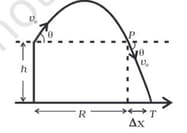
A gun can fire shells with maximum speed and the maximum horizontal range that can be achieved is .If a target farther away by distance (beyond ) has to be hit with the same gun as shown in the figure here. Show that it could be achieved by raising the gun to a height at least .
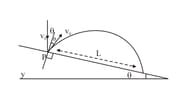
A particle falling vertically from a height hits a plane surface inclined to horizontal at an angle with speed and rebounds elastically as shown in the figure. Find the distance along the plane where it will hit the second time.
A girl riding a bicycle with a speed of towards north direction, observes rain falling vertically down. If she increases her speed to, rain appears to meet her at to the vertical. What is the speed of the rain? In what direction does rainfall as observed by a ground-based observer?
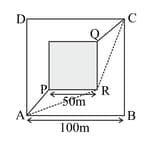
A man wants to reach from to the opposite corner of the square (as in figure) The sides of the square are . A central square of is filled with sand. Outside this square, he can walk at a speed . In the central square, he can walk only at a speed of . What is smallest value of for which he can reach faster via a straight path through the sand than any path in the square outside the sand?
.