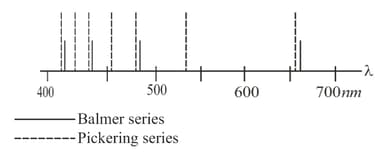
Every other spectral line in one of the spectral series of an ionized helium atom (the Pickering series) closely resembles a line in the Balmer series for hydrogen. What is the principal quantum number of the level to which the electrons transfer when these lines are emitted? Why don't the lines coincide exactly? What is the meaning of the lines that lie in between the lines of the Balmer series?

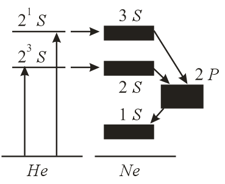
In a$He-Ne$ laser, the helium atoms are excited from the ground state to two sublevels, $2^{1}S$ and $2^{3}S$, interact with $Ne$ atoms, and give off their energy to $Ne$ atoms, with the result that the latter are transferred to the $3S$ and $2S$ levels.

The Ne atoms in these states emit radiation and go over to the $2P$ level. In the figure, the $3S$ and $2S$ levels, each consisting of four sublevels, and the $2P$ level, which consists of ten sublevels, are depicted by broad black bands. In addition to the above-mentioned transitions, a transition from the $3S$ state to the $3P$ level is possible, but we do not show this transition in the figure.

From the $2P$ state, $Ne$ atoms go over to the $1S$ state, and then gradually return to their ground state. Why don't He atoms emit radiation during transitions from the $2^{1}S$ and $2^{3}S$ states directly to the ground state? What must be the relationship between the lifetimes of He atoms in states $3S,2S$, and $2P$ for continuous generation of radiation to be possible? It has been established that of the two transitions, $3S\to 2P$ and $2S\to 2P$, one is accompanied by radiation in the visible spectrum and the other, in the IR spectrum. Which transition corresponds to which spectrum?

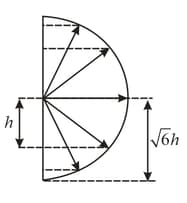
The angular momentum of electrons in an atom and this spatial orientations can be depicted schematically by a vector diagram where the length of the vector is proportional to the absolute value of the orbital angular momentum of an electron. What vectors in the diagram correspond to the minimal value of the principal quantum number $n$ and what are the values of the quantum numbers $l$ and $m ?$ 

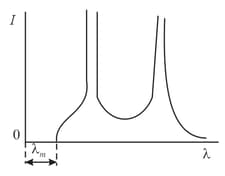
The intensity distribution of $X$-ray radiation over wavelengths consists of a continuous spectrum, which is limited from the short-wave side by a limit wavelength ${\lambda }_m$, and a characteristic spectrum, which consists of separate peaks. In the figure (with an arbitrary scale) we depict such a distribution for a voltage $U_1$ applied to the $X$-ray tube. How will the distribution change if the voltage is decreased three-fold, that is, $U_2=\left(\frac{1}{3}\right)U_1 ?$ 

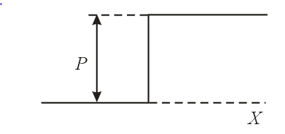
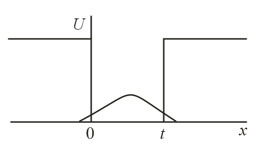
An electron is inside a potential well with vertical walls. The electronic wave function is depicted in the figure. Is the depth of the well finite or infinite?

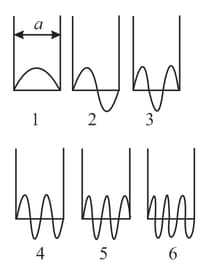
An electron is in motion in a potential well of infinite depth. Depending on the electron kinetic energy, the electronic wave function has different configurations depicted in the figure. Which of these states is retained when the width of the potential well is decreased two-fold? By what factor will the minimal kinetic energy of the electron change in the process?

From the viewpoint of the optical analogy of the wave properties of an electron, the regions of space where it possesses different potential energies may be interpreted as regions with different refractive indices. In the figure two such regions are depicted, the regions are separated by a boundary where the potential energy$P$ experiences a jump. In which of these regions is the refractive index greater? In which of the two cases, when the electron moves from left to right or when it moves from right to left, will the phase of the wave function be retained under reflection of the electron from the barrier, and in which will it change to its opposite?