Explain converse of theorem on angle between tangent and secant with an example.

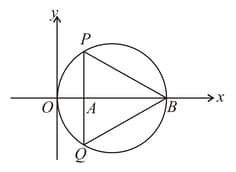
Prove that, “the lengths of the two tangent segments to a circle drawn from an external point are equal”.

Suppose $S_1 \mathrm{a}\mathrm{n}\mathrm{d} S_2$ are two unequal circles; $AB$ and $CD$ are the direct common tangents to these circles. A transverse common tangent $PQ$ cuts $AB$ in $R$ and $CD$ in $S$. If $AB=10$ units, then $RS$ is -

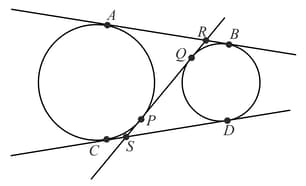
On the circle with center $O$, points $A,B$ are such that $OA = AB$. A point $C$ is located on the tangent at $B$ to the circle such that $A$ and $C$ are on the opposite sides of the line $OB$ and $AB=BC$. The line segment $AC$ intersects the circle again at $F$. Then the ratio $\angle BOF:\angle BOC$ is equal to -

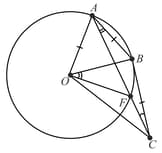
In the following figure, point ‘$A$’ is the centre of the circle. Line $MN$ is tangent at point $M$. If $AN=10 \mathrm{cm}$ and $MN=6 \mathrm{cm}$, determine the radius of the circle.

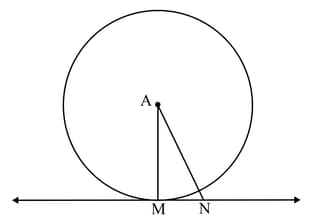
If the angle between two radii of a circle is $130°$, the angle between the tangents at the ends of radii is

If two tangents inclined at an angle of $60°$are drawn to a circle of radius $3 \mathrm{c}\mathrm{m},$ then length of each tangent is equal to

In the figure, $\mathrm{PQ}$ and $\mathrm{PR}$ are two tangents to a circle with centre $\mathrm{O}$. If $\mathrm{\angle }\mathrm{Q}\mathrm{P}\mathrm{R}=46°,$ then $\mathrm{\angle }\mathrm{Q}\mathrm{O}\mathrm{R}$ is
 

​​​​​​​

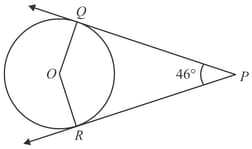
From a point $\mathrm{P}$ which is at a distance $13 \mathrm{c}\mathrm{m}$ from the centre $\mathrm{O}$ of a circle of radius $5 \mathrm{c}\mathrm{m},$ the pair of tangents $\mathrm{PQ}$ and $\mathrm{PR}$ to the circle are drawn. Then the area of the quadrilateral $\mathrm{PQOR}$ is

If $\mathrm{PA}$ and $\mathrm{PB}$ are tangents to the circle with centre $\mathrm{O}$ such that $\angle \mathrm{A}\mathrm{P}\mathrm{B}=50°,$ then $\angle \mathrm{O}\mathrm{A}\mathrm{B}$ is equal to