MEDIUM

Earn 100

Explain the relationship between uniform circular motion and SHM.

Important Questions on Oscillations

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to

A

and

T

, respectively. At time

t = 0

one particle has displacement

A

while the other one has displacement

- \frac{A}{2}

and they are moving towards each other. If they cross each other at time

t

, then

t

is:

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

For particle $P$ revolving round the centre $O$ with radius of circular path $r$ and regular velocity $ω$ , as shown in below figure, the projection of $O P$ on the $x$ -axis at time $t$ is

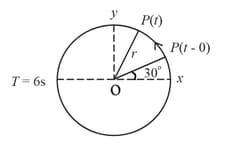
Question Image

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

If we tie a stone to the end of a string and move it with a constant angular speed in a horizontal plane about fixed point, the stone would perform a :

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A stone is swinging in a horizontal circle

0.8 m

in diameter, at

30 rev \min^{- 1}

. A distant light causes a shadow of the stone to be formed on a nearby wall. What is the amplitude of the motion of the shadow? What is the frequency?

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A particle is in a uniform circular motion around origin. What is the angle made by the position vector of the particle with the X-axis, when its displacement along the X-axis becomes half the maximum displacement?

HARD

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

The x-projection for a certain particle in circular motion under SHM with period of

2 s

, amplitude of oscillation is

2 m

and initial phase of

\frac{π}{2}

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A stone is swinging in a horizontal circle

1 m

in diameter at

60 rev \min^{- 1}

. A distant light causes a shadow of the stone to be formed on a nearly vertical wall. The amplitude and period of motion for the shadow of the stone are,

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A particle executes SHM with time period

T

and amplitude

A

. The maximum possible average velocity in time

T / 4

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

The circular motion of a particle with constant speed is

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A particle executes simple harmonic motion between

x = - A a n d x = + A

. The time taken for it to go from 0 to

A / 2 i s T_{1}

and to go from

A / 2 t o A i s T_{2}

. Then

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A particle is revolving in a circular path with gradually increasing speed. Its motion is

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

If the particle is moving in circular motion under SHM, then its x-projection is depending upon

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

The value of phase at maximum displacement from the mean position of a particle in S.H.M. is

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

Suppose a particle P is moving uniformly on a circle of radius A with the angular speed

ω

. The sense of rotation is anticlockwise. If the

t = 0

, it makes an angle of

ϕ

with the positive direction of the x-axis. In time

t

, it will cover a further angle

ω t

.What is the projection of position vector on the X-axis at time

t

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A particle executes simple harmonic motion between

x = - A a n d x = + A

. The time taken for it to go from 0 to

A / 2 i s T_{1}

and to go from

A / 2 t o A i s T_{2}

. Then

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

Two particles are performing simple harmonic motion in a straight line about the same equilibrium point. The amplitude and time period for both particles are same and equal to

A

and

T

, respectively. At time

t = 0

one particle has displacement

A

while the other one has displacement

- \frac{A}{2}

and they are moving towards each other. If they cross each other at time

t

, then

t

is:

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the $x$ -projection of the radius vector of the rotating particle $P$ is :

(Given, time period of revolution $T = 30 s)$

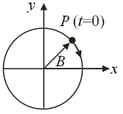
Question Image

HARD

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A particle is moving in a uniform circular motion on a horizontal surface. Particle's position and velocity at time $t = 0$ are shown in the figure in the coordinate system. Which of the indicated variable on the vertical axis is/are correctly matched by the graph(s) shown alongside for particle's motion?

Question Image

EASY

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A particle is moving in a uniform circular motion on a horizontal surface. Particle position and velocity at time $t = 0$ are shown in the figure in the coordinate system. Which of the indicated variable on the vertical axis is incorrectly matched by the graph shown alongside for particle's motion-
Question Image

MEDIUM

Physics>Oscillations and Waves>Oscillations>Simple Harmonic Motion as a Projection of Uniform Circular Motion

A particle is performing simple harmonic motion along

x - axis

with amplitude

4 cm

and time period

1.2 \sec

. The minimum time taken by the particle to move from

x = + 2 cm

x = + 4 cm

and back again is given by:

Explain the relationship between uniform circular motion and SHM.

Important Questions on Oscillations

Learn and Prepare for any exam you want !