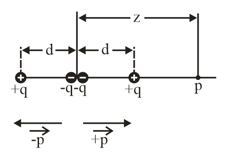
Figure shows a generic electric quadrupole. It consists of two dipoles with dipole moments that are equal in magnitude but opposite in direction. Show that the value of $E$ on the axis of the quadrupole for a point $P$ at a distance $z$ from its center (assume $z\gg d$ ) is given by, $E=\frac{3Q}{4\pi {\epsilon }_0{z}^4}$ in which $Q \left(=2q{d}^2\right)$ is known as the quadrupole moment of the charge distribution. 

Suppose you design an apparatus in which a uniformly charged disk of radius $R$ is to produce an electric field. The field magnitude is most important along the central perpendicular axis of the disk at a point $P$ at distance $2.00R$ from the disk (figure a). Cost analysis suggests that you switch to a ring of the same outer radius $R$ but with inner radius, $\frac{R}{4.00}$ (figure b). Assume that the ring will have the same surface charge density as the original disk. If you switch to the ring, by what percentage will you decrease the electric field magnitude at $P?$

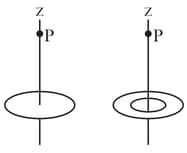
     (a)                                          (b)

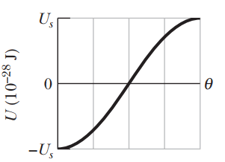
A certain electric dipole is placed in a uniform electric field $\overrightarrow{E}$ of magnitude $50 \mathrm{N} {\mathrm{C}}^{-1}$. Figure gives the potential energy $U$ of the dipole versus the angle $\theta$ between $\overrightarrow{E}$ and the dipole moment $\overrightarrow{p}$. The vertical axis scale is set by $U_{\mathrm{s}}=100\times {10}^{-28} \mathrm{J}$. What is the magnitude of $\overrightarrow{p}$?

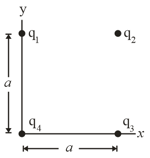
In figure, the four particles form a square of edge length, $a=5.00$ $\mathrm{cm}$ and have charges $q_1=+30 \mathrm{nC}, q_2=$$-15 \mathrm{nC}, q_3=+15 \mathrm{nC},$ and $q_4=-30 \mathrm{nC}$. In unit-vector notation, what net electric field do the particles produce at the square's center?

An electron with a speed of $2.60\times {10}^{8 }\mathrm{cm} {\mathrm{s}}^{-1}$ enters an electric field of magnitude $1.00\times {10}^3 \mathrm{N} {\mathrm{C}}^{-1}$, traveling along a field line in the direction that retards its motion. (a) How far will the electron travel in the field before stopping momentarily and (b) how much time would have elapsed? (c) If the region containing the electric field is $8.00 \mathrm{mm}$ long $($too short for the electron to stop within it), what fraction of the electron's initial kinetic energy will be lost in that region?

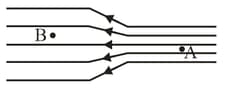
In figure, the electric field lines on the left have twice the separation of those on the right. (a) If the magnitude of the field at $A$ is $60 \mathrm{N} {\mathrm{C}}^{-1}$, what is the magnitude of the force on a proton at $A$? (b) What is the magnitude of the field at $B$?