Figure shows a wedge of mass $2 \mathrm{kg}$ resting on a frictionless floor. A block of mass $1 \mathrm{kg}$ is kept on the wedge and the wedge is given an acceleration of $5 \mathrm{m} {\mathrm{s}}^{-2}$ towards right. Then

 

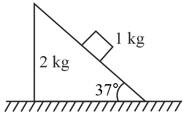
A triangular block of mass $M$ rests on a smooth surface as shown in figure. A cubical block of mass $m$ rests on the inclined surface. If all surfaces are frictionless, the force that must be applied to $M$ so as to keep $m$ stationary relative to $M$ is

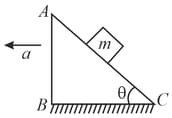
A block of mass $m$ resting on a wedge of angle $\theta$ as shown in the figure. The wedge is given an acceleration a towards left. What is the minimum value of $a$ due to external agent so that the mass $m$ falls freely?

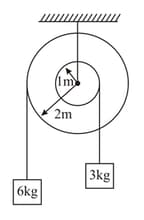
The moment of inertia of the pulley system as shown in the figure is$3 \mathrm{kg} – {\mathrm{m}}^2 .$ The radii of bigger and smaller pulleys are $2\mathrm{m} \mathrm{and} 1\mathrm{m}$respectively. As the system is released from rest, find the angular acceleration of the pulley system. (Assume that there is no slipping between string & pulley and string is light) $[\mathrm{Take} g=10 \mathrm{m} {\mathrm{s}}^{-2} ]$

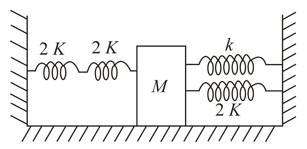
Four massless springs whose force constants are $2k\text{,} 2k\text{,} k \text{and} 2k$, respectively are attached to a mass $M$ kept on a frictionless plane (as shown in figure). If the mass $M$ is displaced in the horizontal direction, then the frequency of the system,

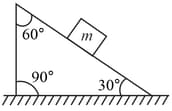
A fixed wedge with both surfaces inclined at $45°$ to the horizontal as shown in the figure. A particle $P$ of mass $m$ is held on the smooth plane by a light string that passes over a smooth pulley $A$ and attached to a particle $Q$ of mass $3m$ which rests on the rough plane. The system is released from rest. Given that the acceleration of each particle is of magnitude $\frac{g}{5\sqrt{2}}$ then

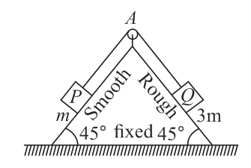
the tension in the string is :

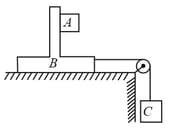
In the arrangement shown mass of the block $B$ and $A$ are $2 \mathrm{m}$ and, $8 \mathrm{m}$ respectively. Surface between $B$ and floor is smooth. The block $B$ is connected to block $C$ by means of a pulley. If the whole system is released then the minimum value of the mass of the block $C$ so that the block $A$ remains stationary with respect to $B$ is: (Coefficient of friction between $A$ and $B$ is $\mathrm{\mu }$ and pulley is ideal)

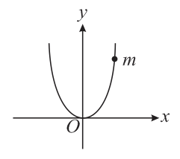
A bead of mass $m$ is located on a parabolic wire, equation( $x^2=ay$) with its axis vertical and vertex directed downward as shown in the figure. If the coefficient of friction is $\mathrm{\mu }$, the highest distance above the x-axis at which the particle will be in equilibrium.