Figure shows the force- extension graphs for four springs, A, B, C and D.

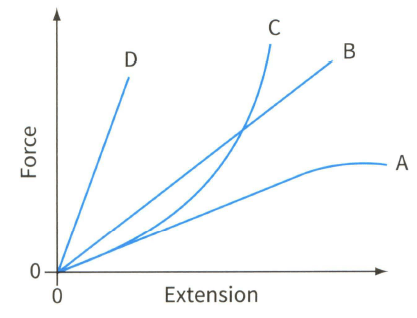
Force-extension graphs for four different springs.

(a) State which spring has the greatest value of force constant.

Figure shows the force- extension graphs for four springs, A, B, C and D.

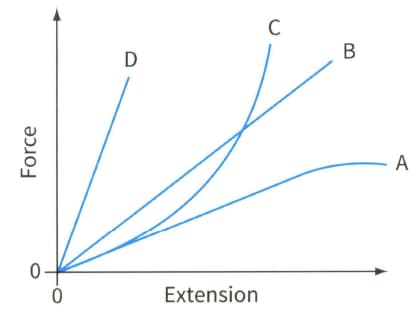
Force-extension graphs for four different springs.

(b) State which is the least stiff.

Figure shows the force- extension graphs for four springs, A, B, C and D.

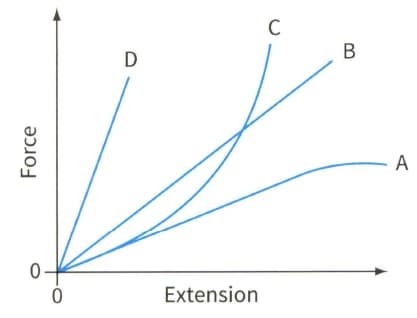
Force-extension graphs for four different springs.

(c) State which of the four springs does not obey Hooke's law.

List the metals in Table from stiffest to least stiff.

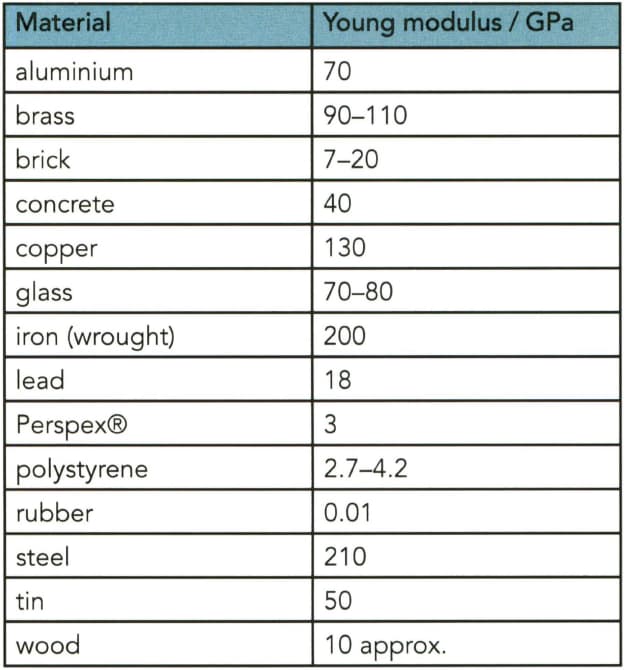
The Young modulus of various materials. Many of these values depend on the precise composition of the material concerned. $\left(\text{Remenber} 1\mathrm{GPa}={10}^9\mathrm{Pa}\right)$

Which of the non-metals in Table is the stiffest?

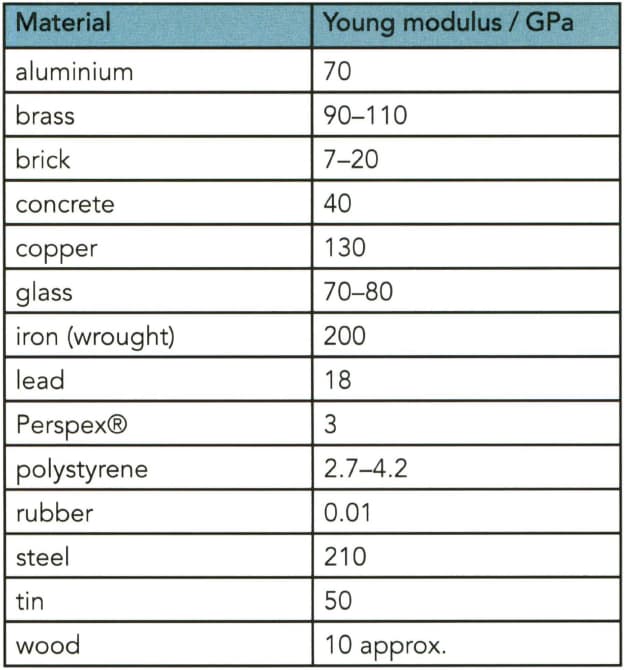
The Young modulus of various materials. Many of these values depend on the precise composition of the material concerned.$\left(\text{Remenber} 1\mathrm{GPa}={10}^9\mathrm{Pa}\right)$

Figure shows stress- strain graphs for two materials, A and B. Use the graphs to determine the Young modulus of each material.

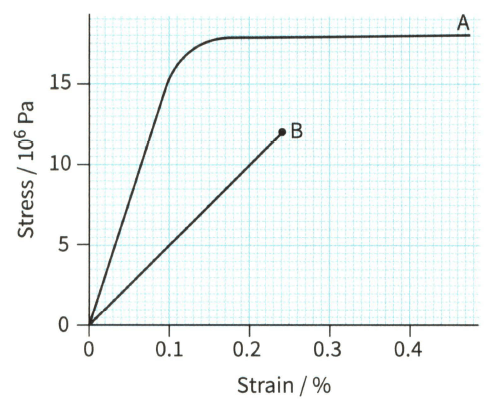
Stress-strain graphs for two different materials.

In an experiment to measure the Young modulus of glass, a student draws out a glass rod to form a fibre $0.800 \mathrm{m}$ in length. Using a travelling microscope, she estimates its diameter to be $0.40 \mathrm{mm}$. Unfortunately, it proves impossible to obtain a series of readings for load and extension. The fibre snaps when a load of $1.00 \mathrm{N}$ is hung on the end. The student judges that the fibre extended by no more than $1 \mathrm{mm}$ before it snapped. Use these values to obtain an estimate for the Young modulus of the glass used. Explain how the actual or accepted value for the Young modulus might differ from this estimate.