MEDIUM
Earn 100

Figures shows the vibrations of four air column. The ratio of frequencies np:nq:nr :ns is


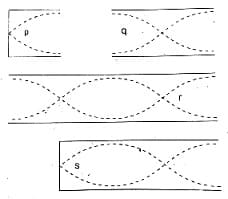
Question Image

50% studentsanswered this correctly

Important Questions on Sound Waves

MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A closed organ pipe has a fundamental frequency of 1.5 kHz. The number of overtones that can be distinctly heard by a person with this organ pipe will be (Assume that the highest frequency a person can hear is 20,000 Hz).
EASY
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A cylindrical tube, open at both the ends has fundamental frequency n . If one of the ends is closed, the fundamental frequency will become
HARD
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A pipe of length 85 cm is closed from one end. Find the number of possible natural oscillations of air column in the pipe whose frequencies lie below 1250 Hz. The velocity of sound in air is 340 m/s.
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
The number of possible natural oscillations of air column in a pipe closed at one end of length 85 cm whose frequencies lies below 1250 Hz are: (velocity of sound =340 ms-1)
HARD
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
The end correction of a resonance column is 1 cm. If the shortest length resonating with the tuning fork is 10 cm, the next resonating length should be
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A one metre long (both ends open) organ pipe is kept in a gas that has double the density of air at STP. Assuming the speed of sound in air at STP is 300 m/s, the frequency difference between the fundamental and second harmonic of this pipe is __________ Hz.
EASY
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
The two nearest harmonics of a tube closed at one end and open at other end are 220 Hz and 260 Hz. What is the fundamental frequency of the system?
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
If sound travels in air with the speed of 340 m s-1, then the number of tones present in an open organ pipe of length 2 m for a maximum frequency of 1200 Hz, are
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
The second overtone of an open organ pipe has the same frequency as the first overtone of a closed pipe which is  L meter long. The length of the open pipe will be
EASY
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
The fundamental frequency of an air column in a pipe closed at one end is 100 Hz. If the same pipe is open at both the ends, the frequencies produced in Hz are
EASY
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
Two nearest harmonics of an organ pipe open at both the ends are 200Hz and 240Hz The fundamental frequency is
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A resonance tube is old and has a jagged end. It is still used in the laboratory to determine the velocity of sound in air. A tuning fork of frequency 512 Hz produces first resonance when the tube is filled with water to a mark 11 cm below a reference mark, near the open end of the tube. The experiment is repeated with another fork of frequency 256 Hz which produces first resonance when water reaches a mark 27 cm below the reference mark. The velocity of sound in air, obtained in the experiment, is close to
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A stationary tuning fork is in resonance with an air column in a pipe. If the tuning fork is moved with a speed of 2 m s-1 in front of the open end of the pipe and parallel to it, the length of the pipe should be changed for the resonance to occur with the moving tuning fork. If the speed of sound in air is 320 m s-1, the smallest value of the percentage change required in the length of the pipe is ________.
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A pipe open at both ends has a fundamental frequency f in air. The pipe is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now:
EASY
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
Tube A has both ends open while tube B has one end closed. Otherwise, they are identical. The ratio of fundamental frequency of tube A and B is,
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A pipe open at one end has length 0.8 m. At the open end of the tube a string 0.5 m long is vibrating in its 1st overtone and resonates with fundamental frequency of pipe. If tension in the string is 50 N, the mass of string is (speed of sound =320 m s-1)
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
On closing an open organ pipe from one end, it is noticed that the frequency of third harmonic is 50 Hz more than the fundamental frequency of vibration in open organ pipe. The fundamental frequency of open organ pipe is
MEDIUM
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
A pipe of 1 m length is closed at one end. Taking the speed of sound in air as 320 m s-1, the air column in the pipe cannot resonate for the frequency in Hz
EASY
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
The fundamental frequency of a closed organ pipe of length 20 cm is equal to the second overtone of an organ pipe open at both the ends. The length of the organ pipe open at both the ends is
EASY
Physics>Oscillations and Waves>Sound Waves>Formation of Standing Waves in an Air Column
An air column, closed at one end and open at the other, resonates with a tuning fork when the smallest length of the column is 50  cm . The next larger length of the column resonating with the same tuning fork is: