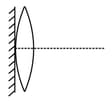
Find equivalent focal length due to combination of two convex lens are in contact having a focal length both of them $30 \mathrm{cm}$.

Two identical equiconvex lenses, each of focal length $f$ are placed side by side in contact with each other with a layer of water in between them as shown in the figure. If refractive index of the material of the lenses is greater than that of water, how the combined focal length $F$ is related to $f ?$

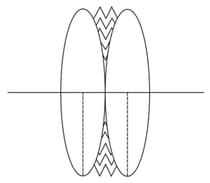
Curved surfaces of a plano-convex lens of refractive index ${\mu }_1$ and a plano-concave lens of refractive index ${\mu }_2$ have equal radius of curvature as shown in figure. Find the ratio of radius of curvature to the focal length of the combined lenses

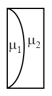
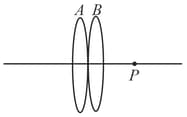
Two convex lenses $A$ & $B$ placed in contact form the image of a distant object at $P.$ If the lens $B$ is moved to the right a little, the image will

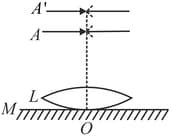
Deduce the equivalent focal length of two convex lenses of focal lengths ${\mathrm{f}}_1\mathrm{and} {\mathrm{f}}_2$, when placed in contact.

For two thin lenses kept in contact with each other, show that:

$\frac{1}{F}=\frac{1}{f_1}+\frac{1}{f_2}$

where the terms have their usual meaning.