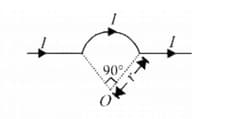
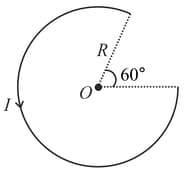
Find the magnetic induction at point O, if the current carrying wire is in the shape shown in the figure.
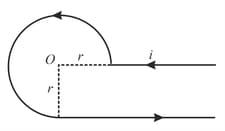
Important Questions on Magnetic Effects of Electric Current
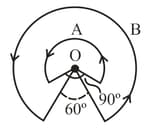
A wire , bent in the shape of an arc of a circle, carrying a current of and having radius and another wire , also bent in the shape of an arc of a circle, carrying a current of and having radius of , are placed as shown in the figure. The ratio of the magnetic fields due to the wires and at the common centre is:
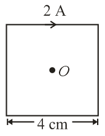
The magnetic field at the centre of the current-carrying square loop shown in the figure is
What is the magnetic field at the centre of arc in the figure below?
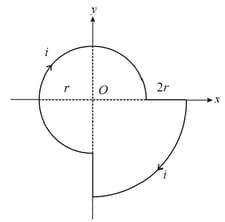
The magnetic field at the centre in the given figure is
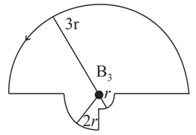
An arrangements with a pair of quarter circular coils of radii and with a common centre and carrying a current is shown.
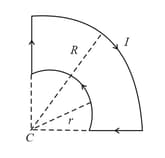
The permeability of free space is . The magnetic field at is
Figure below shows three circuits consisting of concentric circular arcs and straight radial lines. The center of the circle is shown by the dot. Same current flows through each of the circuits. If are the magnitudes of the magnetic field at the center. Which of the following is true?
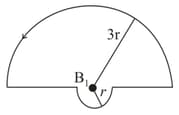
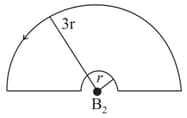
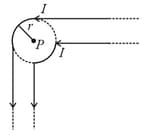
The magnetic field at the point is