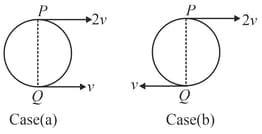
Find the position of instantaneous centre of rotation and angular velocity of the disc in the following cases as shown. Radius of disc is $R$ in each case.

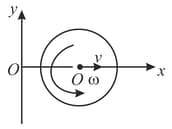
A rotating disc moves in the positive direction of $x$ -axis as shown. Find the equation $y\left(x\right)$ describing the position of the instantaneous axis of rotation if at the initial moment the centre $C$ of the disc was located at origin after which

(a) it moved with constant acceleration $\text{'}a\text{'}$ (initial velocity zero) while the disc rotating anticlockwise with constant angular velocity $\omega .$
(b) it moved with constant velocity $v$ while the disc started rotating anticlockwise with a constant angular acceleration $\alpha$ (with initial angular velocity zero).

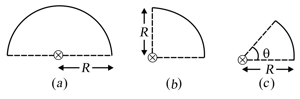
Find out the moment of inertia of the circular ares shown each having mass $M$, radius $R$ and having uniform mass distribution about an axis passing through the centre and perpendicular to the plane.

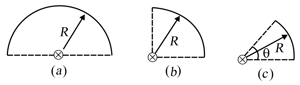
Calculate the moments of inertia of the figures shown, each having uniform mass distribution about an axis perpendicular to the plane and passing through the centre.

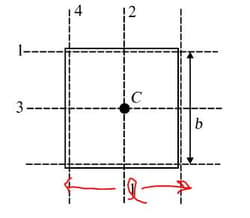
In figure, find moment of inertia of a plate having mass $M$, length $l$ and width $b$ about axes $\mathrm{1,2},3$ and $4$. Assume that $C$ is the centre and mass is uniformly distributed.

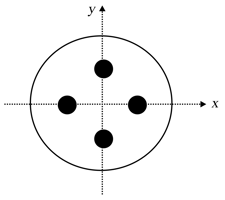
A uniform disc of mass $m$ and radius $R$ has an additional rim of mass $m$ as well as four symmetrically placed masses, each of mass $m/4$, tied at positions $R/2$ from the centre as shown in figure. What is the total moment of inertia of the disc about an axis perpendicular to the disc through its centre?

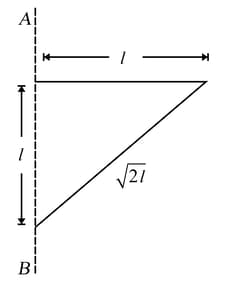
Find moment of inertia of a triangular lamina of mass $M$ about the axis of rotation $AB$ shown in figure.

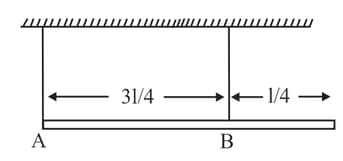
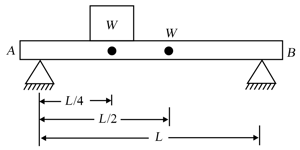
A beam of weight $W$ supports a block of weight $W.$ The length of the beam is $L$ and weight is at a distance $L/4$ from the left end of the beam. The beam rests on two rigid supports at its ends. Find the reactions of the supports.

A uniform rod of length $l$ and mass $m$ is hung from two strings of equal length from a ceiling as shown in figure. Determine the tensions in the strings.