Find the time period of small oscillations of the following systems.

(a) A meter stick suspended through the $20 \mathrm{cm}$ mark.

(b) A ring of mass $\mathrm{m}$ and radius $\mathrm{r}$ suspended through a point on its periphery.

(c) A uniform square plate of edge $\mathrm{a}$ suspended through a corner.

(d) A uniform disc of mass $\mathrm{m}$ and radius $\mathrm{r}$ suspended through a point $r/2$ away from the Centre.

A hollow sphere of radius $2 \mathrm{cm}$ is attached to an $18 \mathrm{cm}$ long thread to make a pendulum. If the time period of oscillation of this pendulum is $\alpha \mathrm{s}$ and it differ from the time period calculated using the formula for a simple pendulum is $\beta \%$?

Find $\alpha +\beta$.

A closed circular wire hung on a nail in a wall undergoes small oscillations of amplitude $2^{°}$ and time period $2 s$. Find

(a) the radius of the circular wire,

(b) the speed of the particle the farthest away from the point of suspension as it goes through its mean position,

(c) the acceleration of this particle as it goes through its mean position and

(d) the acceleration of this particle when it is at an extreme position. (Take $g={\pi }^2 \mathrm{m} {\mathrm{s}}^{-2}$)

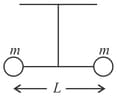
Two small balls, each of mass $m$ are connected by a light rigid rod of length $L$. The system is suspended from its centre by a thin wire of torsional constant $k ,$ The rod is rotated about the wire through an angle ${\theta }_0$ and released. The force exerted by the rod on one of the balls as the system passes through the mean position is ${\left[\frac{k^2{\theta }_0^4}{L^2}+m^2{g}^2\right]}^n$. Find the value of $\mathrm{n}.$

​​​​​​​ 

A particle is subjected to two simple harmonic motions of same time period in the same direction. The amplitude of the first motion is $3.0 \mathrm{cm}$ and that of the second is $4.0 \mathrm{cm}$. Find the resultant amplitude if the phase difference between the motions is

(a) $0^{°}$

(b) ${60}^{\circ }$

(c) ${90}^{\circ }$