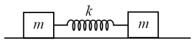Find the time period of the oscillation of mass $m$ in $a, b, c$. The equivalent spring constant of the first pair of springs is $n\pi \sqrt{\frac{m}{k_1+k_2}}$. Find $n$.

  

The spring is unstretched when a man starts pulling on the cord. The mass of the block is $M.$ If the man exerts a constant force $F,$ find

(a) the amplitude and the time period of the motion of the block,

(b) the energy stored in the spring when the block passes through the equilibrium position and

(c) the kinetic energy of the block at this position.

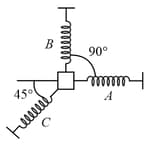
A particle of mass $m$ is attached to three springs $A, B$ and $C$ of equal force constants $k$. If the particle is pushed slightly against the spring $C$ and released, $\pi \sqrt{\frac{m}{bk}}$ is the time period of oscillation. Find the value of $b$.

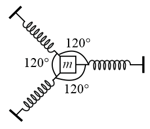
A particle of mass $m$ is attached to three springs $A, B$ and $C$ of equal force constant $k$ as shown in figure. If particle is pushed slowly towards any one spring and released then if the time period of oscillation is$2\pi \sqrt{\frac{\beta m}{3k}}$ find value of $\beta$ .

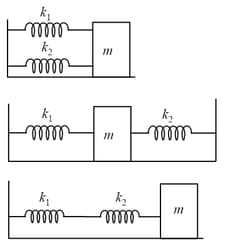
The springs are all unstretched in the beginning, when a man starts pulling the block. The man exerts a constant force $F$ on the block. The frequency of the motion of the block is $\frac{1}{\pi }\sqrt{\frac{k_1{k}_2+k_2{k}_3+k_3{k}_1}{x\left(k_2+k_3\right)}}$. Find the value of $x$.

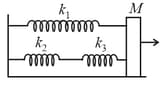
The time period of vertical oscillation of the block is $\pi \sqrt{x\left(\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}\right)}$. Then the value of $x$ is

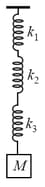
The string, the spring and the pulley are light. If the time period of the mass $m$ is $\beta \pi \sqrt{\frac{m}{k}}$ then what is the value of $\beta$ $?$

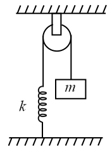
The string and spring are light and the pulley shown in figure has moment of inertia $I$ about its axis, the string does not slip over pulley. Time period of mass is $2\mathrm{\pi }\sqrt{\frac{\left(\mathrm{m}+\mathrm{I}/{\mathrm{R}}^{\mathrm{x}}\right)}{\mathrm{k}}}$. The value of $\mathrm{x}$ is:

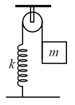
Consider the situation. If the blocks are displaced slightly in opposite directions and released, they will execute simple harmonic motion. The time period of oscillation is $2\pi \sqrt{\frac{m}{C}}$. Then the value of $C$ is: