Flux passing through the shaded surface of a sphere when a point charge $q$ is placed at the center is (radius of the sphere is $R$)

A uniformly charged and infinitely long line having a linear charge density $\mathrm{\lambda }$ is placed at a normal distance $y$ from a point $O$. Consider a sphere of radius $R$ with $O$ as the center and $R>y$. Electric flux through the surface of the sphere is

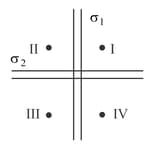
Two infinite sheets having charge densities ${\mathrm{\sigma }}_1$ and ${\mathrm{\sigma }}_2$ are placed in two perpendicular planes whose two-dimensional view is shown in the figure. The charges are distributed uniformly on the sheets in electrostatic equilibrium condition. Four points are marked $\mathrm{I}\text{,} \mathrm{I}\mathrm{I}\text{,} \mathrm{I}\mathrm{I}\mathrm{I}$ and $\mathrm{I}\mathrm{V}$. The electric field intensities at these points are ${\overrightarrow{\mathrm{E}}}_1\text{,}{\overrightarrow{ \mathrm{E}}}_2\text{,} {\overrightarrow{\mathrm{E}}}_3$ and ${\overrightarrow{\mathrm{E}}}_4$, respectively. The correct expression for the electric field intensities is

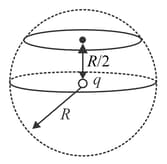
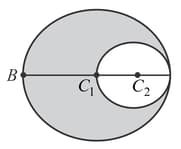
A positively charged sphere of radius $r_0$ carries a volume charge density $\mathrm{\rho }$ (figure). A spherical cavity of radius $\frac{r_0}{2}$ is then scooped out and left empty. ${\mathrm{C}}_1$ is the center of the sphere and ${\mathrm{C}}_2$ that of the cavity. What is the direction and magnitude of the electric field at point $\mathrm{B}$?

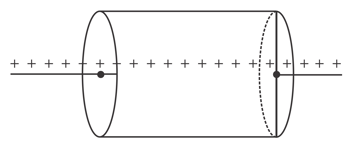
Consider an infinite line charge having uniform linear charge density and passing through the axis of a cylinder. What will be the effect on the flux passing through the curved surface if the portions of the line charge outside the cylinder is removed.

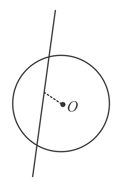
One-fourth of a sphere of radius $R$ is removed as shown in the figure. An electric field $E$ exists parallel to the $xy$ plane. Find the flux through the remaining curved part.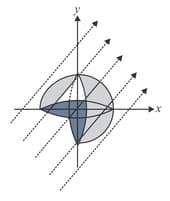

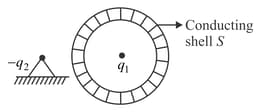
The negative charge $-q_2$ is fixed while positive charge $q_1$ as well as the conducting sphere $S$ is free to move (refer figure). If the system is released from rest,