HARD
Earn 100
For a certain transverse standing wave on a long string, an antinode is formed at and next to it, a node is formed at . The position of the string particle at is shown in figure.
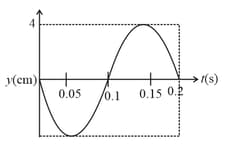
(a)Transverse displacement of the particle at and is cm
(b)Transverse displacement of the particle at and is
(c)Speed of the travelling waves that interfere to produce this standing wave is
(d)The transverse velocity of the string particle at and is
50% studentsanswered this correctly
Important Questions on Sound Waves
EASY
HARD
EASY
EASY
MEDIUM
EASY
MEDIUM
EASY
MEDIUM
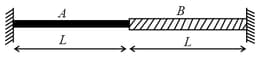
MEDIUM
(All quantities are in units.)
EASY
HARD
EASY
HARD
MEDIUM
The electric field of a plane electromagnetic wave is given by . Its magnetic field will be given by
MEDIUM
A closed pipe of length contains some sand. A speaker is connected at one of its ends. The frequency of the speaker at which the sand will arrange itself in equidistant piles is close to (velocity of sound is )
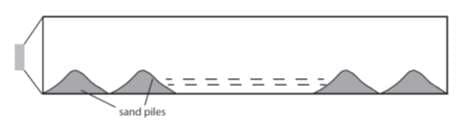
EASY
MEDIUM
MEDIUM
EASY

