HARD

Earn 100

For a diatomic gas change in internal energy for unit change in temperature for constant pressure and constant volume is U₁ and U₂ respectively. U₁ : U₂ is

50% studentsanswered this correctly

Important Questions on Thermodynamics

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

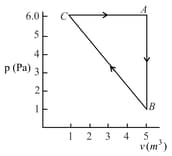
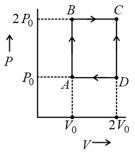
For the given cyclic process $C A B$ as shown for a gas, the work done is:

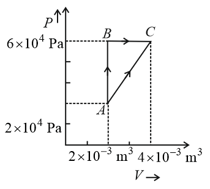
Question Image

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

A gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then:

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

Half mole of an ideal monoatomic gas is heated at a constant pressure of

1 atm

from

20 ° C

90 ° C

. Work done by the gas is

(

Gas constant,

R = 8.21 J {mol}^{- 1} K^{- 1}

)

EASY

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

Figure below shows two paths that may be taken by a gas to go from a state A to a state C.
Question Image

In process AB,

400 J

of heat is added to the system and in process BC,

100 J

of heat is added to the system. The heat absorbed by the system in the process AC will be:

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

The initial pressure and volume of a given mass of an ideal gas with $(\frac{C_{p}}{C_{V}} = γ)$ , taken in a cylinder fitted with a piston, are $p_{0}$ and $V_{0}$ respectively. At this stage the gas has the same temperature as that of the surrounding medium which is $T_{0} .$ It is adiabatically compressed to a volume equal to $\frac{V_{0}}{2} .$
Subsequently the gas is allowed to come to thermal equilibrium with the surroundings. What is the heat released to the surrounding?

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

An ideal gas goes through a reversible cycle

a \to b \to c \to d

has the V - T diagram shown below. Process

d \to a a n d b \to c

are adiabatic.

Question Image

The corresponding P - V diagram for the process is (all figures are schematic and not drawn to scale) :

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

A gas is enclosed in a cylinder with a movable frictionless piston. Its initial thermodynamic state at pressure

P_{i} = 10^{5} Pa and volume V_{i} = 10^{- 3} m^{3}

changes to a final state at

P_{f} = (\frac{1}{32}) \times 10^{5} Pa and V_{f} = 8 \times 10^{- 3} m^{3}

in an adiabatic quasi-static process, such that

P^{3} V^{5} =

constant. Consider another thermodynamic process that brings the system from the same initial state to the same final state in two steps: an isobaric expansion at

P_{i}

followed by an isochoric (isovolumetric) process at volumes

V_{f}

. The amount of heat supplied to the system in the two step process is approximately

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

An engine operates by taking

n

moles of an ideal gas through the cycle

A B C D A

shown in figure. The thermal efficiency of the engine is:

(Take

C_{v} = 1.5 R

, where

R

is gas constant)

Question Image

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

In the given $P - V$ diagram, a monoatomic gas $(γ = \frac{5}{3})$ is first compressed adiabatically from state $A$ state $B$ . Then it expands isothermally from state $B$ to state $C$ . [Given : ${(\frac{1}{3})}^{0.6} = 0.5, \ln 2 \approx 0.7$ ].

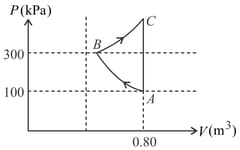
Question Image

Which of the following statement(s) is(are) correct?

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

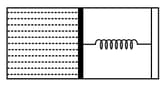
An ideal gas of density $ρ = 0.2 kg m^{- 3}$ enters a chimney of height $h$ at the rate of $α = 0.8 kg s^{- 1}$ from its lower end, and escapes through the upper end as shown in the figure. The cross-sectional area of the lower end is $A_{1} = 0.1 m^{2}$ and the upper end is $A_{2} = 0.4 m^{2}$ . The pressure and the temperature of the gas at the lower end are $600 Pa$ and $300 K$ , respectively, while its temperature at the upper end is $150 K$ . The chimney is heat insulated so that the gas undergoes adiabatic expansion. Take $g = 10 m s^{- 2}$ and the ratio of specific heats of the gas $γ = 2$ . Ignore atmospheric pressure.

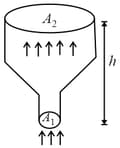
Question Image

Which of the following statement(s) is(are) correct?

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

One mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true?

Question Image

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

One mole of a monoatomic ideal gas goes through a thermodynamic cycle, as shown in the volume versus temperature

(V - T)

diagram. The correct statement(s) is/are:

[

R

is the gas constant]
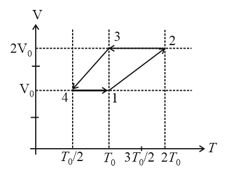
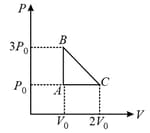
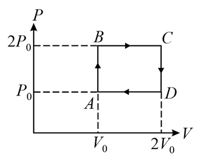
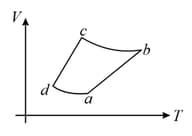
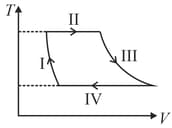
Question Image

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

One mole of an ideal monatomic gas is taken along the path

A B C A

as shown in the

P - V

diagram. The maximum temperature attained by the gas along the path

B C

is given by:
Question Image

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

The above

P - V

diagram represents the thermodynamic cycle of an engine, operating with an ideal mono-atomic gas. The amount of heat, extracted from the source in a single cycle, is:

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

One mole of an ideal monatomic gas undergoes a process described by the equation

P V^{3} =

constant. The heat capacity of the gas during this process is

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

Two moles of an ideal monoatomic gas occupies a volume $V$ at $27^{o} C$ . The gas expands adiabatically to a volume $2 V$ . Calculate $(a)$ the final temperature of the gas and $(b)$ change in its internal energy.

MEDIUM

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

A monoatomic gas is compressed from a volume of

2 m^{3}

to a volume of

1 m^{3}

at a constant pressure of

100 N m^{2}

. Then it is heated at constant volume by supplying

150 J

of energy. As a result, the internal energy of the gas

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

Consider a spherical shell of radius R at temperature T. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume

u = \frac{U}{V} \propto T^{4}

and pressure

p = \frac{1}{3} (\frac{U}{V})

. If the shell now undergoes an adiabatic expansion the relation between T and R is:

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

A mixture of ideal gas containing

5

moles of monatomic gas and

1

mole of rigid diatomic gas is initially at pressure

P_{0},

volume

V_{0}

and temperature

T_{0} .

If the gas mixture is adiabatically compressed to a volume

\frac{V_{0}}{4}

, then the correct statement(s) is/are,
(Given

2^{1.2} = 2.3; 2^{3.2} = 9.2; R

is gas constant)

HARD

Physics>Thermal Physics>Thermodynamics>First Law of Thermodynamics and Its Applications (Only for Ideal Gases)

An ideal monoatomic gas is confined in a horizontal cylinder by a spring loaded piston (as shown in the figure). Initially the gas is at temperature

T_{1}

, pressure

P_{1}

and volume

V_{1}

and the spring is in its relaxed state. The gas is then heated very slowly to temperature

T_{2}

, pressure

P_{2}

and volume

V_{2}

. During this process the piston moves out by a distance

x

. Ignoring the friction between the piston the cylinder, the correct statement(s) is (are)

Question Image

For a diatomic gas change in internal energy for unit change in temperature for constant pressure and constant volume is U1 and U2 respectively. U1 : U2 is

Important Questions on Thermodynamics

Learn and Prepare for any exam you want !

For a diatomic gas change in internal energy for unit change in temperature for constant pressure and constant volume is U₁ and U₂ respectively. U₁ : U₂ is