For a given curved surface of a right circular cone when the volume is maximum, prove that the semi vertical angle is .

Important Questions on Application of Derivatives
Suppose, is a function satisfying the following conditions
has a minimum value at , and
(c) for all
where are some constants. Determine the constants and the function .
Consider the function, . Find
(a) The and intercept of if they exist.
(b) Derivatives and .
(c) The interval on which is an increasing and the intervals on which is decreasing.
(d) Relative maximum and minimum points.
(e) Any inflection point.
The function defined for all real numbers has the following properties
and for some constant . Find
(a) the intervals on which is increasing and decreasing and any local maximum or minimum values.
(b) the intervals on which the graph is concave down and concave up
(c) the function and plot its graph.
The graph of the derivative of a continuous function is shown with
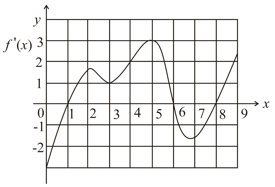
(i) On what intervals, is increasing or decreasing?
(ii) At what values of does have a local maximum or minimum?
(iii) On what intervals, is concave upward or downward?
(iv) State the -coordinate(s) of the point(s) of inflection.
(v) Assuming that , sketch a graph of .
