EASY
Earn 100
For a uniformly charged thin spherical shell, the electric potential radially away from the centre of shell can be graphically represented as

(a)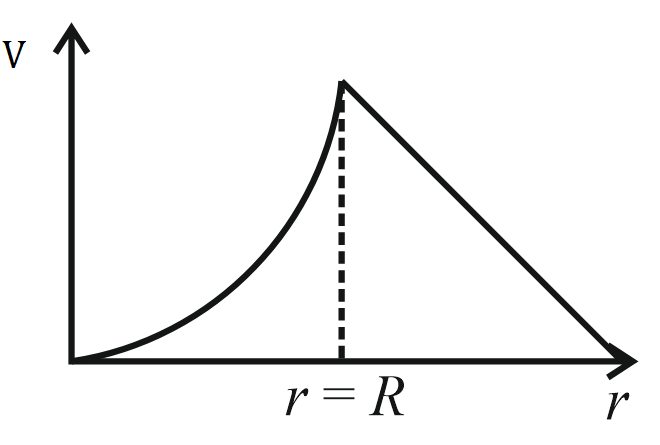

(b)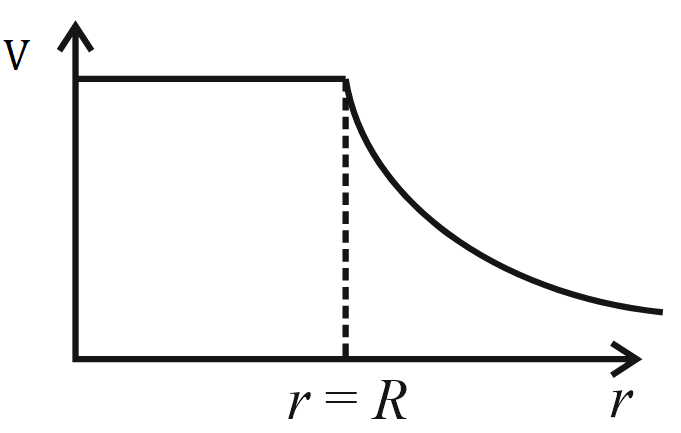

(c)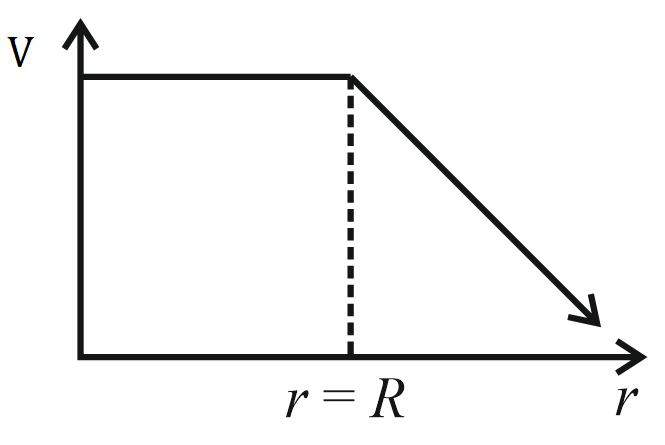

(d)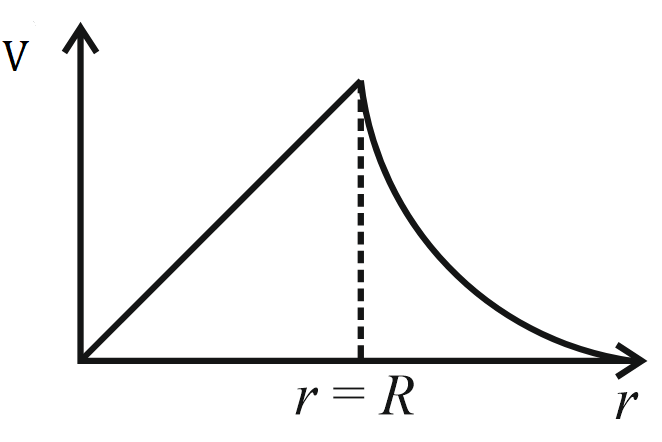

78.77% studentsanswered this correctly
Important Questions on Electrostatics
HARD
EASY
EASY
EASY
MEDIUM
EASY
EASY
EASY
HARD
EASY
A charge Q is distributed over two concentric conducting thin spherical shells radii and . If the surface charge densities on the two shells are equal, the electric potential at the common centre is :
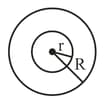
MEDIUM
Four point charge (with equal magnitude of charge of but with different signs) are placed at four corners of a square of side Assuming that the square is centered at the origin and the configuration of the charges are as given in the figure, the potential and the magnitude of electric field at the origin, respectively are
[Note
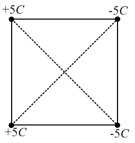
MEDIUM
The total potential at a point at distance from their common centre, where would be:
EASY
EASY
MEDIUM
MEDIUM
EASY
EASY
HARD
EASY

