For given spring-mass system, If the time period of small oscillations of block about its mean position is $\pi \sqrt{\frac{nm}{k}}$, then find $n$. Assume ideal conditions. The system is in a vertical plane and take $k_1=2k, k_2=k.$

In the figure shown the spring is relaxed and mass m is attached to the spring. The spring is compressed by $2A$ and released at $t= 0$. Mass $m$ collides with the wall and loses two-third of its kinetic energy and returns. Starting from $t= 0$, find the time taken by it to come back to rest again (instant at which spring is again under maximum compression). Take $\sqrt{\frac{m}{K}}=\frac{12}{\pi }$

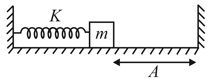
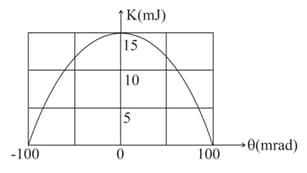
Figure shows the kinetic energy $K$ of a simple pendulum versus its angle $\mathrm{\theta }$ from the vertical. The pendulum bob has mass $0.2 \mathrm{kg}$. If the length of the pendulum is equal to $\frac{\mathit{n}}{\mathit{g}}$ meter, then find $n (g = 10 \mathrm{m} {\mathrm{s}}^{-2}).$

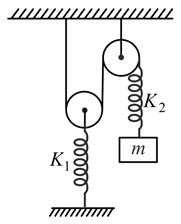
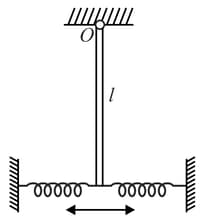
If the angular frequency of small oscillations of a thin uniform vertical rod of mass $m$ and length $l$ hinged at the point $\mathrm{O}$ (Fig.) is $\sqrt{\frac{n}{l}}$, then find $\mathrm{n}$. The force constant for each spring is $K/2$ and take $K=\frac{2mg}{l}.$ The springs are of negligible mass. $(g= 10 \mathrm{m} {\mathrm{s}}^{-2})$

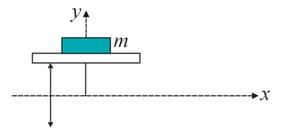
As shown in the figure a horizontal platform with a mass $m$ placed on it is executing SHM along $y$-axis. If the amplitude of oscillation is $2.5 \mathrm{cm}$, the minimum period of the motion for the mass not to be detached from the platform is: $(g= 10 \mathrm{m} {\sec }^{-2} = {\mathrm{\pi }}^2)$