EASY

JEE Main/Advanced

IMPORTANT

Earn 100

Gas $P$ follow the van der Waal's equation of state. Select the correct statement about this gas (Assume $P \to 0$ )

50% studentsanswered this correctly

Important Points to Remember in Chapter -1 - States of Matter from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

1. Introduction:

The characteristics of any of the three states of matter depend on the energies of the molecules and the way the molecules of the substance aggregate. Therefore, it is necessary for a chemist to know the physical laws which govern the behaviour of the matter in different states, particularly the liquid and the gaseous states.

2. The three States of Matter:

(i) Solid state $\to$ possesses a definite shape, size, and mass.

(ii) Liquid state $\to$ possesses a definite volume, a definite mass but no definite shape.

(iii) Gaseous state $\to$ possesses neither shape nor size.

Note:

(a) Fourth state (Plasma State):

A superheated gaseous state, consisting of a mixture of electrons and positively charged ions, only found at high temperatures such as the interior of the sun.

(b) Fifth state:

Refers to the super-cooled solids in which atoms lose their separate identity, get condensed, and behave like a single super atom.

3. Measurable Properties of Gases:

(i) Volume: Gases tend to occupy all available space. So, the volume of a gas is equal to the volume of the container.

(ii) Temperature: It is the degree of the hotness and the coldness.

Conversion of $° C$ to $K : T (i n K) = T (i n ° C) + 273$ .

(iii) Pressure: It is the force exerted by a gas per unit area.

$1 a t m = 760 m m$ of $H g = 760 t o r r = 1.01 \times 10^{5} P a$ .

$1 b a r = 10^{5} P a$ .

4. Intermolecular Forces:

	Force	Interaction	Force or energy (r = the distance between two particles)	Extent of force	Example	Strength	Effect in physical properties
1	Dispersion (or) London force	Between two non-polar atoms or molecules	Interaction energy $\propto \frac{1}{r^{6}}$	Increases with an increase in the molecular mass.	Halogen, noble gases	Weakest	Low boiling liquids or gases at room.
2	Dipole- Dipole forces	Between two polar molecules	Interaction energy $\propto \frac{1}{r^{3}}$	Increases with an increase in the molecular mass and the polarity.	$R - X,$ $R - O - R^{'}$ $R - {C H}_{2} - R,$ $R - C H O$	Stronger	The boiling point increases.
3	Dipole- Induced Dipole forces	Between polar and non - polar species	Interaction energy $\propto \frac{1}{r^{6}}$	Increases with an increase in the polarity of molecule and the size or the polarizability of the non-polar molecule.	The solubility of noble gases and halogens in water is due to these. forces	Weaker than dipole-dipole forces but stronger than dispersion. forces.	The solubility Increases.
4	Hydrogen Bonding	Between hydrogen attached to small and highly electronegative element and neighbouring group or neighbouring molecule.	Interaction energy $\propto \frac{1}{r^{n}} (n < 3)$	Increases with an increase in the electronegativity of the element to which the hydrogen atom is attached.	$H - F, H_{2} O$	Stronger than dipole- dipole interaction.	The boiling point increases.

5. Gaseous Laws and Ideal Gas Equation:

(i) Boyle’s law:

$V \propto \frac{1}{P} (n, T = c o n s t)$

$P_{1} V_{1} = P_{2} V_{2}$

(ii) Charle’s law:

$V \propto T (n, P = c o n s t)$

$\frac{V_{2}}{V_{1}} = \frac{T_{2}}{T_{1}}$

(iii) Gay Lussac’s law:

$P \propto T (n, V = c o n s t)$

$\frac{P_{2}}{P_{1}} = \frac{T_{2}}{T_{1}}$

(iv) Avogadro’s law:

$V \propto$ moles $\propto$ number of molecules $(P, T = c o n s t a n t)$

(v) Ideal gas equation:

$P V = n R T$

$R = 0.0821$ litre atm ${m o l}^{- 1} K^{- 1}$ .

$R = 8.314 J K^{- 1} {m o l}^{- 1}$ or $8.314 N \times {m K}^{- 1} {m o l}^{- 1} .$

$R = 2$ cal $K^{- 1} {m o l}^{- 1}$ .

$R = 8.314 \times 10^{7} {e r g K}^{- 1} {m o l}^{- 1}$ .

The relationship between the density, the molecular mass, the temperature, and the pressure of a gaseous substance.

We know that for an ideal gas:

$P V = n R T; n = \frac{m}{M},$ where $m =$ mass of the gas, $M =$ molecular mass of the gas.

$P V = \frac{m}{M} R T$ (or) $M = \frac{m}{V} \frac{R T}{P}$

i.e., $M = d \frac{R T}{P}$ , where $d = \frac{m}{V}$ i.e., the density of the gas.

6. Dalton's Law of Partial Pressure:

$P_{mixture} = P_{1} + P_{2} + P_{3} \dots \dots \dots . . (T & V const) P_{1}, P_{2} and P_{3} are partial pressures of gas 1, 2 and 3 respectively .$

$P_{m o i s t g a s} = P_{d r y g a s} + P_{w a t e r v a p o u r s}$

(i) From the ideal gas equation:

$P_{A} V = n_{A} R T$ and $P_{B} V = n_{B} R T$

(ii) In the form of mole fraction:

$P_{A} = X_{A} P_{T} = \frac{n_{A}}{n_{T}} P_{T} X_{A} + X_{B} = 1$

$P_{B} = X_{B} P_{T} = \frac{n_{B}}{n_{T}} P_{T}$

$P_{T} =$ The sum of the partial pressure of all gases.

(iii) In the form of the volume fraction:

$P_{A} = \frac{V_{A}}{V} P_{T} a n d P_{B} = \frac{V_{A}}{V} P_{T}$

(iv) If the individual pressure and the individual volume are given:

$P_{A} = \frac{V_{A}}{V} P_{1} a n d P_{B} = \frac{V_{B}}{V} P_{2}$

$P_{1}, P_{2} =$ The pressure of the gases before mixing.

$P_{A}, P_{B} =$ The pressure of the gases after mixing.

7. Kinetic Theory of Gases and Molecular Speeds (The important postulates of the theory are):

(i) All gases are made up of a very large number of extremely small particles called molecules.

(ii) The molecules move randomly with high speed. During their motion, they collide with one another and against the walls of the container.

(iii) The pressure of the gas is due to the bombardment of the gas molecules against the walls of the container.

(iv) The molecules are separated from one another by large spaces so that the actual volume occupied by the molecules is negligible, compared to the total volume of the gas.

(v) There is no force of attraction between the molecules.

(vi) The molecular collisions are perfectly elastic. There is no loss or gain of kinetic energy.

(vii) The average kinetic energy of the molecules is directly proportional to the absolute temperature.

The pressure exerted by a gas $P = \frac{1}{3} \frac{{mnc}^{2}}{V}$ .

$m \to$ mass of each molecule, $n \to$ number of molecules, $c \to$ root mean square velocity, $V \to$ volume of the gas.

8. Distribution of Molecular Speeds:

During collision, the molecules exchange the energy; thereby they change their speed and kinetic energy. Therefore, at any instant, the different molecules have different speeds and hence, different kinetic energy. But a fraction of molecules with a particular speed remains constant. This is known as the distribution of speeds. This is also known as the Maxwell – Boltzmann distribution law.

Important features of Maxwell's distribution curve:

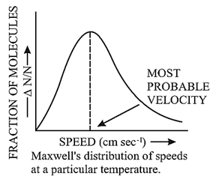
Question Image

(i) The fraction of molecules with very low or very high speeds is very small.

(ii) The maximum fraction of the molecules possesses a velocity corresponding to peak in the curve, called the most probable speed.

(iii) The molecular motion can be described in $3$ different types of speed. They are:

a. Most Probable Speed $(α)$ : This is the speed which is possessed by the maximum fraction of the gas molecules at a given temperature.

$α = \sqrt{\frac{2 R T}{M}}$ M is the molecular mass of the gas.

b. Average Speed $(u_{a v})$ : This is the average of the speed of the different molecules in a gas at a particular temperature.

If $V_{1}, V_{2}, V_{3}$ … are the speeds of $n_{1}, n_{2}, n_{3}, \dots$ molecules of the gas, then
$u_{a v} = \frac{n_{1} V_{1} + n_{2} V_{2} + n_{3} V_{3} + \dots}{n_{1} {+ n}_{2} + n_{1} + \dots}$

Average speed is also given by the expression:

$u_{a v} = \sqrt{\frac{8 R T}{π M}}$

Root mean Square speed $(C) :$ : It is the square root of the mean of the squares of the speeds of the different molecules in a gas at a given temperature.
$C = \sqrt{\frac{n_{1} V_{1} + n_{2} V_{2} + n_{3} V_{3} + \dots}{n_{1} + n_{2} + n_{1} + \dots}}$

Root mean square speed is given by the expression:

$c = \sqrt{\frac{3 R T}{M}}$ or $\sqrt{\frac{3 P V}{M}}$

Note: The relation between the different types of speeds

$α : u_{a v} : c ∷ 1 : 1.28 : 1.224 .$

9. Graham's Diffusion Law:

"Under similar conditions of temperature and pressure, the rates of the diffusion of gases are inversely proportional to the square roots of their densities".

$r α \sqrt{\frac{1}{d}},$ where $r =$ rate of diffusion and $d = d e n s i t y$

$\frac{r_{1}}{r_{2}} = \sqrt{\frac{d_{2}}{d_{1}}} = \sqrt{\frac{M_{2}}{M_{1}}} (∴ V \cdot D = \frac{M}{2})$

$r_{1} = \frac{V_{1}}{t_{1}} r_{2} = \frac{V_{2}}{t_{2}}$

$∴ \frac{r_{1}}{r_{2}} = \frac{\frac{V_{1}}{t_{1}}}{\frac{V_{2}}{t_{2}}} = \sqrt{\frac{d_{2}}{d_{1}}} = \sqrt{\frac{M_{2}}{M_{1}}}$

When $V_{1} = V_{2} = V \frac{r_{1}}{r_{2}} = \frac{t_{2}}{t_{1}} = \sqrt{\frac{d_{2}}{d_{1}}} = \sqrt{\frac{M_{2}}{M_{1}}}$

Similarly, if $t_{1} = t_{2} = t$

$\frac{r_{1}}{r_{2}} = \frac{V_{1}}{V_{2}} = \sqrt{\frac{d_{2}}{d_{1}}} = \sqrt{\frac{M_{2}}{M_{1}}}$

10. Van der Waal’s Equation:

A plot of $P V - P$ at a constant temperature for several gases shows deviations from the ideal behaviour. Therefore, $P V = n R T$ cannot be applied to these gases. Thus, another equation must be sought in order to correlate $P, V, T$ for these gases, which is Van der Waal’s equation.

$(P + \frac{n^{2} a}{V^{2}}) (\lor - n b) = n R T$

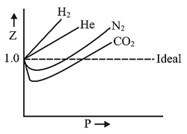
Question Image

Causes of deviation:

There are two objectionable postulates in the kinetic theory of gases.

(i) The volume of a molecule is negligible as compared to the total volume of the gas. Actually, gas molecules do possess some volume which accounts for the deviation. Hence, the total volume of the gas is not equal to the volume of the vessel.

(ii) There is no intermolecular force of attraction between gaseous molecules. (There exists a force of attraction between gaseous molecules otherwise liquefaction of gases would be impossible). By correcting these two postulates, we get an equation which can be applied to the gases which deviate from the ideal behaviour.

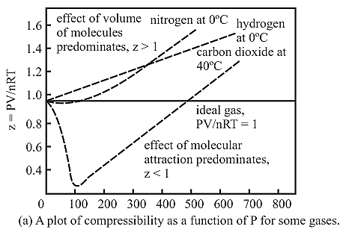
11. Compressibility Factor:

The deviation of a gas from the ideal behaviour can also be expressed in terms of the compressibility factor $(Z)$ .

$Z = \frac{P V}{R T} [f o r 1 m o l e]$

If $z = 1$ , the gas shows ideal gas behaviour.

If $z > 1$ , the gas shows positive deviation.

If $z < 1$ , the gas shows negative deviation.

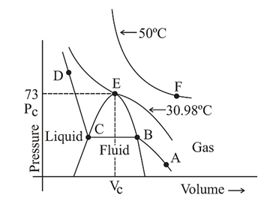
Question Image

12. Liquefaction of Gases:

A plot of pressure against volume at a constant temperature (isotherm) based on experimental observation done for carbon dioxide is given by Andrew. The observations are as follows:

(i) At a high temperature, isotherm is the same as that of an ideal gas. Therefore, no gas can be liquefied at a high temperature even at a very high pressure.

(ii) At $30.68 ° C, {C O}_{2}$ remains a gas up to $73 a t m$ pressure. Liquid ${C O}_{2}$ appears exactly at $73 a t m$ at $30.98 ° C$ . This temperature is called the critical temperature of ${C O}_{2}$ . Further increase in the pressure simply compresses the liquid ${C O}_{2}$ and the curve represents the compressibility of the liquid ${C O}_{2}$ .

(iii) At $21.5 ° C, {C O}_{2}$ remains gas only up to the point $B$ . At $B$ , liquid of a particular volume appears. On further compression, the pressure remains constant till the point $C$ is reached. This is because the liquid and the gaseous ${C O}_{2}$ coexist at equilibrium and more gas condenses. Further compression results in a steep rise in the pressure.

(iv) Point $D$ represents a liquid state and any point under the dome shaped area represents the existence of liquid and gaseous ${C O}_{2}$ in equilibrium.

(v) All the gases, upon compression at a constant temperature, (isothermal compression) show the same behaviour as shown by ${C O}_{2}$ .

(vi) It can be observed that gases should be cooled below their critical temperature for liquefaction. Liquefaction of permanent gases requires cooling as well as considerable compression.

Compression brings the molecules in close vicinity and cooling slows down the movement of the molecules. Therefore, the intermolecular interactions may hold them closely and the gas liquefies.

(vii) It is possible to change a gas into a liquid and vice versa by a process in which always a single phase exists. This can be done by compression at the critical temperature.

(viii) At the critical temperature, liquid passes into a gaseous state continuously and the surface separating the two phases disappears. In this state, the component is said to be in a fluid state.

It is the state of a substance where the liquid and the gaseous forms of the substance cannot be distinguished. In the fluid state, the liquid and the gaseous forms of the substance exist in equilibrium. The area under the dome in the graph represents fluid state.

(ix) Liquefaction of a gas is possible only below its critical temperature.

Question Image

13. Concept of Critical Temperature:

The effect of the temperature on conversion of a gas into a liquid is more than that of the pressure. It was confirmed by Thomas Andrew in the conversion of gaseous ${C O}_{2}$ to liquid ${C O}_{2}$ .

(i) Critical temperature $(T_{C})$ :

The temperature at which or below which a gas can be converted into a liquid by applying pressure.

If the temperature of the gas is above this temperature, thus it cannot be converted into a liquid, however high the pressure applied is.

(ii) Critical pressure $(P_{c})$ :

The pressure required to liquify the gas at the critical temperature is called the critical pressure.

(iii) Critical volume $(V_{c})$ :

The volume of $1$ mole of a gas at the critical temperature and the critical pressure is called critical volume.

The relationship between critical constants and Van der Waals constants:

(i) $V_{c} = 3 b$

(ii) $P_{C} = \frac{a}{27 b^{2}}$

(iii) $T_{c} = \frac{8 a}{27 R b}$

(iv) Critical compressibility factor, $Z_{C} = \frac{P_{C} V_{C}}{R T_{C}} = \frac{3}{8} = 0.375$ .

14. Vapour Pressure of a Liquid:

(i) Evaporation:

When a liquid is taken in an open container, slowly it escapes into the gas phase. This is known as evaporation. This is explained in terms of the kinetic molecular models. The molecules in a liquid are held with strong intermolecular forces, but the fraction of molecules which are having high kinetic energy will overcome this force of attraction and escape from the liquid phase to the gaseous phase.

(ii) Evaporation causes cooling:

During evaporation, the molecules with a high kinetic energy will escape from the liquid phase, leaving behind the molecules with a low energy. Hence, the temperature decreases.

(iii) Factors affecting the rate of evaporation:

(a) Nature of liquid.

(b) Temperature.

(d) Blowing the current of air across the surface of the liquid.

(iv) Vapour pressure:

The pressure of the vapour, when the vapour is in equilibrium with its liquid at a given temperature. When a liquid is heated in a closed vessel, with an increase in the vapour pressure, a homogeneous mixture of the liquid and the gaseous form of the substance is obtained. This state is called a fluid state.

(v) Boiling point:

The temperature at which the vapour pressure of the liquid is equal to the atmospheric pressure is called boiling point. At $1$ atm pressure, the boiling temperature is called the normal boiling point. If the pressure is 1 bar, the boiling point is called the standard boiling point of the liquid.

Note:

(a) Water boils at a lower temperature in hill stations. This is because at higher altitudes, the atmospheric pressure is low. Therefore, even at a low temperature, the vapour pressure of the liquid becomes equal to the external pressure and the liquid boils.

(b) Food gets cooked in less time in a pressure cooker because inside the pressure cooker, the pressure is higher and the water boils at a higher temperature. So, more heat is supplied to the food.

15. Surface Tension of Liquid:

(i) Surface tension $(γ)$ :

"Surface tension is defined as the downward force experienced by the molecules of a liquid perpendicular to the plane of its surface.” Surface tension is also defined as the energy required to increase the surface area of the liquid by one unit.

To understand surface tension, let us consider two molecules, the molecule $A$ well within the bulk of the liquid and the molecule $B$ at the surface of the liquid. The molecule $' A^{'}$ is attracted by the surrounding molecules equally and the net effect is zero, whereas the molecule $B$ at the surface is pulled inward by the molecules below it. Consequently, the molecules at the surface experience a resultant inward pull and the surface behaves as if it were under tension.

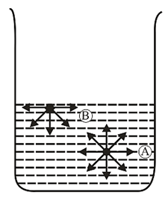
Question Image

Units of surface tension $(γ) : K g s^{- 2}$ or $N m^{- 1}$ .

(ii) Effect of temperature on the surface tension:

With an increase of temperature, the magnitude of interparticle forces decreases and the surface tension decreases.

(iii) Effect of adding surface active solutes:

Addition of ethanol, methanol, soap, detergents etc. to water lowers its surface tension. The cleaning action of soap is based on this effect.

(iv) Effects of surface tension:

(a) Spherical shapes of drops.

(b) Capillary action.

When water is taken in a glass tube, there are cohesive forces between water molecules and adhesive forces between glass and water. In this case, the adhesive forces are stronger relative to the cohesive forces. As a result, water acquires a concave upward surface. Such a curved surface of a liquid is known as meniscus. In case of mercury, the cohesive forces are stronger than the adhesive forces and hence, mercury has a concave downward meniscus.

(v) Some characteristic features of surface tension:

Surface tension gives a spherical shape to drops of a liquid because spheres occupy minimum surface area and hence, minimum energy and maximum stability.

The tendency of a liquid to rise into narrow pores is called capillary action. The liquid rises in the capillary tube due to surface tension. This phenomenon is observed in the plants where water rises through the bark and reaches the leaves.

The stretching property of the liquid is due to the surface tension.

16. Viscosity:

The force of friction in which one part of the liquid offers to another part of the liquid is called viscosity.

$f = - η \frac{\partial v}{\partial x}$ where $η =$ coefficient of viscosity

When $a = 1 {c m}^{2}, v = 1 {c m s}^{- 1}, \partial x = 1 c m$ then $f = η$ .

The coefficient of viscosity $η$ is defined as the force acting per unit area of the liquid when the velocity gradient is one unit.

Various units of coefficient of viscosity $(η) : {N m}^{- 2} s, d y n e {c m}^{- 1} s, K g m^{- 1} s^{- 3}$ , Pascal second, Poise $K g m^{- 1} s^{- 1}$ .

(i) Factors affecting viscosity:

The magnitude of viscosity is directly proportional to the intermolecular attractive forces like hydrogen bonding, Van der Waals forces, and is inversely proportional to the temperature. Intermolecular attractive forces would pull the molecules closer so that the viscosity increases. Increase in the temperature increases the kinetic energy of the molecules. This results in a decrease in the intermolecular attractive forces. Therefore, the viscosity decreases.

(ii) Effect of the temperature:

With the increase in the temperature, the magnitude of interparticle forces decreases and the kinetic energy of the molecules increases. This causes a decrease in the viscosity of the liquid.

17. Joule – Thomson effect:

When a highly compressed gas is allowed to expand into a region of low pressure, the temperature of the gas falls. This is known as the Joule Thomson effect.

Gas P follow the van der Waal's equation of state. Select the correct statement about this gas (Assume P→0)

Important Points to Remember in Chapter -1 - States of Matter from Embibe Experts Gamma Question Bank for Engineering Chemistry Solutions

Learn and Prepare for any exam you want !

Gas $P$ follow the van der Waal's equation of state. Select the correct statement about this gas (Assume $P \to 0$ )