Given an one dimensional system with total energy $E=\frac{{p_x}^2}{2m}+V\left(x\right)=$ constant, where $p_x$ is the $x$ component of the linear momentum and $V\left(x\right)$ is the potential energy of the system. Show that total time derivative of energy gives us force $F_x=-\frac{d}{dx}V\left(x\right)$. Verify Hooke’s law by choosing potential energy $V\left(x\right)=\frac{1}{2}k{x}^2$.

Consider a simple pendulum of length $l=0.9 \mathrm{m}$ which is properly placed on a trolley rolling down on a inclined plane which is at $\theta =45°$ with the horizontal. Assuming that the inclined plane is frictionless, calculate the time period of oscillation of the simple pendulum.

(Answer approximately to the nearest integer)

Consider two simple harmonic motion along x and y axis having same frequencies but different amplitudes as $x=A\sin (\omega t+\varphi )$ (along x-axis) and $y=B\sin \omega t$ (along y-axis).Then show that $\frac{x^2}{A^2}+\frac{y^2}{B^2}-\frac{2xy}{AB}\cos \varphi ={\sin }^2\varphi$.

And also discuss the special cases when $\varphi =0; \varphi =\mathrm{\pi }; \varphi =\frac{\mathrm{\pi }}{2};$$\varphi =\frac{\mathrm{\pi }}{2} \mathrm{and} A=B; \varphi =\frac{\mathrm{\pi }}{4}$.

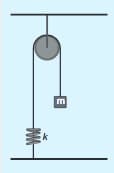
Compute the time period for the following system if the block of mass $m$ is slightly displaced vertically down from its equilibrium position and then released. Assume that the pulley is light and smooth, strings and springs are light.