If one root of the equation $f\left(x\right)=0$ is near to $x_0$, then the first approximation of this root as calculated by Newton Raphson method is the abscissa of the point, where the following straight line intersects the x-axis"

The equation $x^3-7x^2+1=0$ has two positive roots, $\alpha$ and $\beta$, which are such that $\alpha$ lies between $0$ and $1$and $\beta$ lies between $6$ and $7 .$

By deriving two suitable iterative formulae from the given equation, carry out suitable iterations to find the value of $\alpha$ and of $\beta ,$ giving each correct to $2$ decimal places. Give the value of each of your iterations to $4$ decimal places.

The parametric equations of a curve are $x=t^2+6,y=t^4-t^3-5t$. The curve has a stationary point for a value of $t=1.394$.

Hence find the coordinates of the stationary point, giving each coordinate correct to $1$ significant figure.

Represent the union of two sets by Venn diagram for each of the following.

$X=\{x | x$ is a prime number between $80$ and $100\}$

$Y=\{y | y$ is an odd number between $90$ and $100\}$

The equation $cosecx=x^2$ has a root, $\alpha ,$ between $1$ and $2 .$ The equation can be rearranged either as $x={\sin }^{-1}\left(\frac{1}{x^2}\right)$ or $x=\sqrt{\frac{1}{\sin x}}.$

Write down two possible iterative formulae, one based on each given rearrangement. Use the starting value $1.5$

Show that one of the formulae fails to converge.

The sequence of values given by the formula $x_{n+1}=\sqrt{\frac{8{x_n}^2}{3 \sec x_n}},$ with initial value $x_1=1,$ converges to $\alpha .$ Use this formula to calculate $\alpha$ correct to $2$ decimal places, showing the result of each iteration to $4$ decimal places.

The graphs of $y={\left(\frac{3}{2}\right)}^x-1$ and $y=x$ intersect at the points $O(0,0)$ and $A.$

Sketch these graphs on the same diagram.

The equation $cosecx=x^2$ has a root, $\alpha ,$ between $1$ and $2 .$ The equation can be rearranged either as $x={\sin }^{-1}\left(\frac{1}{x^2}\right)$ or $x=\sqrt{\frac{1}{\sin x}}.$

Write down two possible iterative formulae, one based on each given rearrangement. 

The equation $cosecx=x^2$ has a root, $\alpha ,$ between $1$ and $2 .$ The equation can be rearranged either as $x={\sin }^{-1}\left(\frac{1}{x^2}\right)$ or $x=\sqrt{\frac{1}{\sin x}}.$

Write down two possible iterative formulae, one based on each given rearrangement. Use the starting value $1.5$

Show that one of the formulae fails to converge.

Show that the other formula converges to $\alpha$ and find the value of $\alpha$ correct to $3$ decimal places. Give the result of each iteration to $5$ decimal places.

The diagram shows a container in the shape of a cone with a cylinder on top.

The height of the cylinder is $3$ times its base radius, $r.$

The volume of the container must be $5500{ \mathrm{cm}}^3.$ The base of the cone has a radius of $r \mathrm{cm}.$

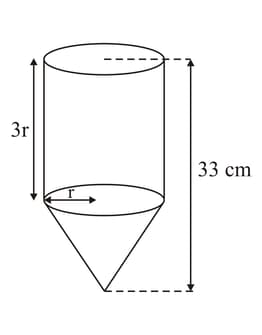
Write down an expression for the height of the cone in terms of $r.$