HARD
10th CBSE
IMPORTANT
Earn 100

If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is

50% studentsanswered this correctly

Important Questions on Some Applications of Trigonometry

HARD
10th CBSE
IMPORTANT
Modern's abc+ of Mathematics for Class 10>Chapter 9 - Some Applications of Trigonometry>FOR ASSESSMENT>Q 18
If the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake is
HARD
10th CBSE
IMPORTANT
Modern's abc+ of Mathematics for Class 10>Chapter 9 - Some Applications of Trigonometry>FOR ASSESSMENT>Q 19
In a rectangle, the angle between a diagonal and a pole is 30° and the length of its diagonal is 8 cm. Then the area of the rectangle is
MEDIUM
10th CBSE
IMPORTANT
Modern's abc+ of Mathematics for Class 10>Chapter 9 - Some Applications of Trigonometry>FOR ASSESSMENT>Q 20
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is:
MEDIUM
10th CBSE
IMPORTANT
Modern's abc+ of Mathematics for Class 10>Chapter 9 - Some Applications of Trigonometry>NATIONAL TALENT SEARCH EXAMINATION (NTSE)>Q 1
A man from the top of a 100 metres high tower sees a car towards the tower at an angle of depression of 30°. After some time, the angle of depression becomes 60°. The distance in metres travelled by the car during this time is
HARD
10th CBSE
IMPORTANT
Modern's abc+ of Mathematics for Class 10>Chapter 9 - Some Applications of Trigonometry>NATIONAL TALENT SEARCH EXAMINATION (NTSE)>Q 2
The upper 34th portion of a vertical pole subtends an angle tan-1(35) at a point in the horizontal plane through its foot and at a distance 40 m from the foot. A possible height of the vertical pole is:
HARD
10th CBSE
IMPORTANT
Modern's abc+ of Mathematics for Class 10>Chapter 9 - Some Applications of Trigonometry>NATIONAL TALENT SEARCH EXAMINATION (NTSE)>Q 3
A person standing on the bank of a river observes that the angle of the top of a tree on the opposite bank of the river is 60° and when he retires 40 metres away from the tree the angle of elevation becomes 30°. The breadth of the river is
HARD
10th CBSE
IMPORTANT
Modern's abc+ of Mathematics for Class 10>Chapter 9 - Some Applications of Trigonometry>NATIONAL TALENT SEARCH EXAMINATION (NTSE)>Q 4

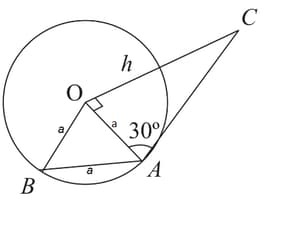
A tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB (=a) subtends an angle of 60° at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30°. The height of the tower is

Question Image

HARD
10th CBSE
IMPORTANT
Modern's abc+ of Mathematics for Class 10>Chapter 9 - Some Applications of Trigonometry>NATIONAL TALENT SEARCH EXAMINATION (NTSE)>Q 5
An observer on the top of a cliff 200 m above the sea leve;, observes the angles of depression of two ships on opposite sides of the cliff to be 45° and 30° respectively. Then the distance between the ships if the line joining these points to the base of the cliff is: