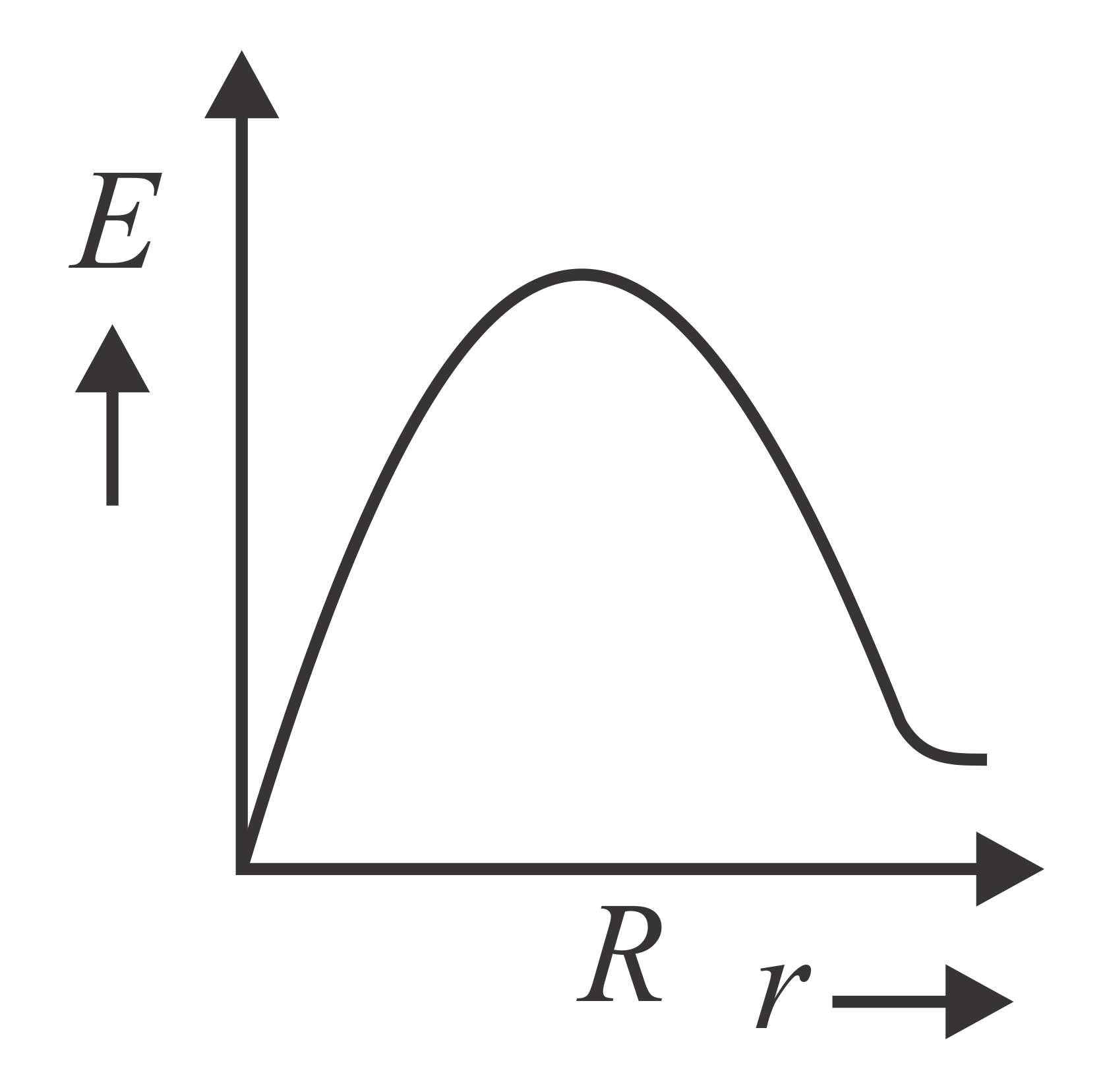
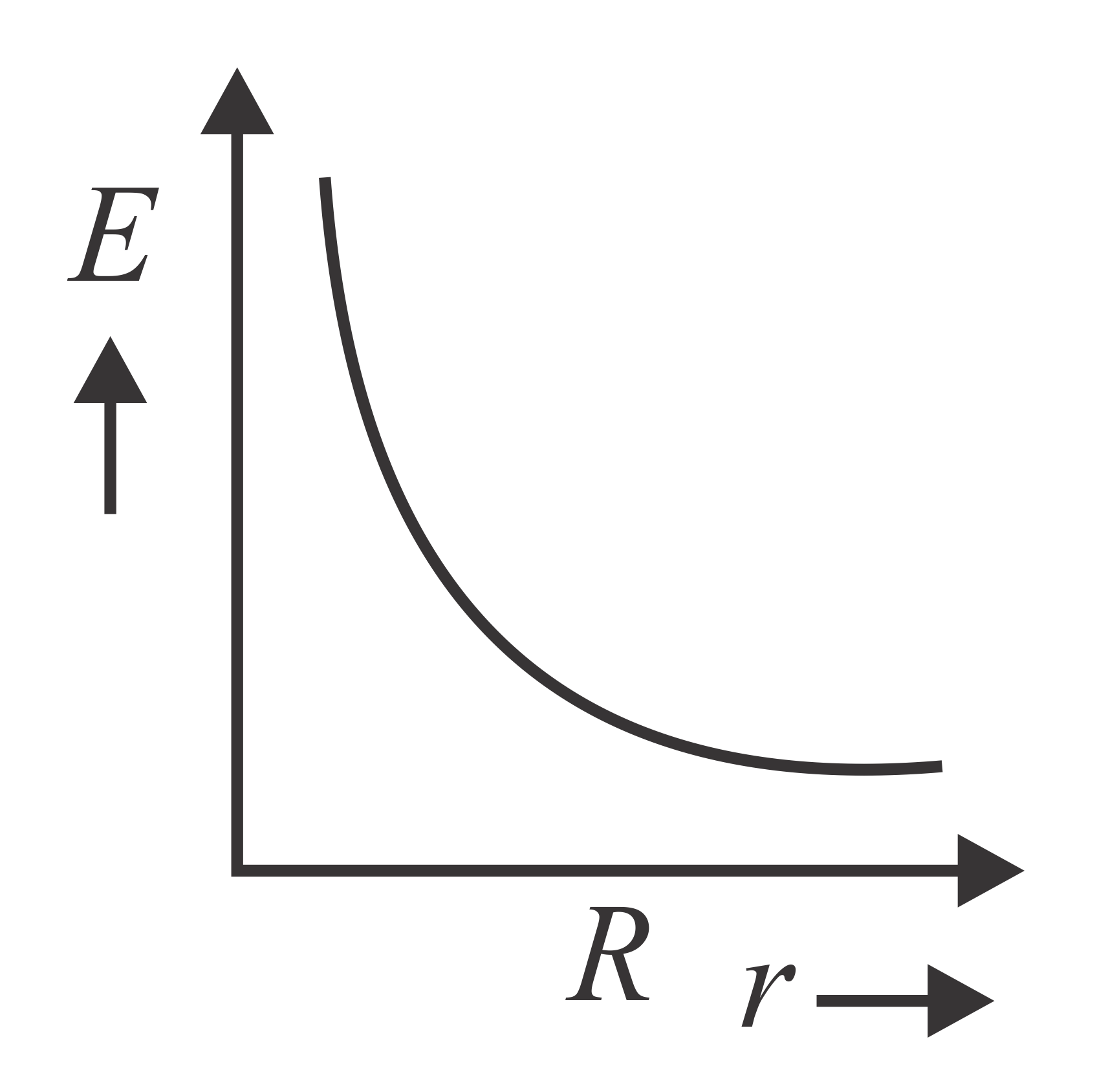
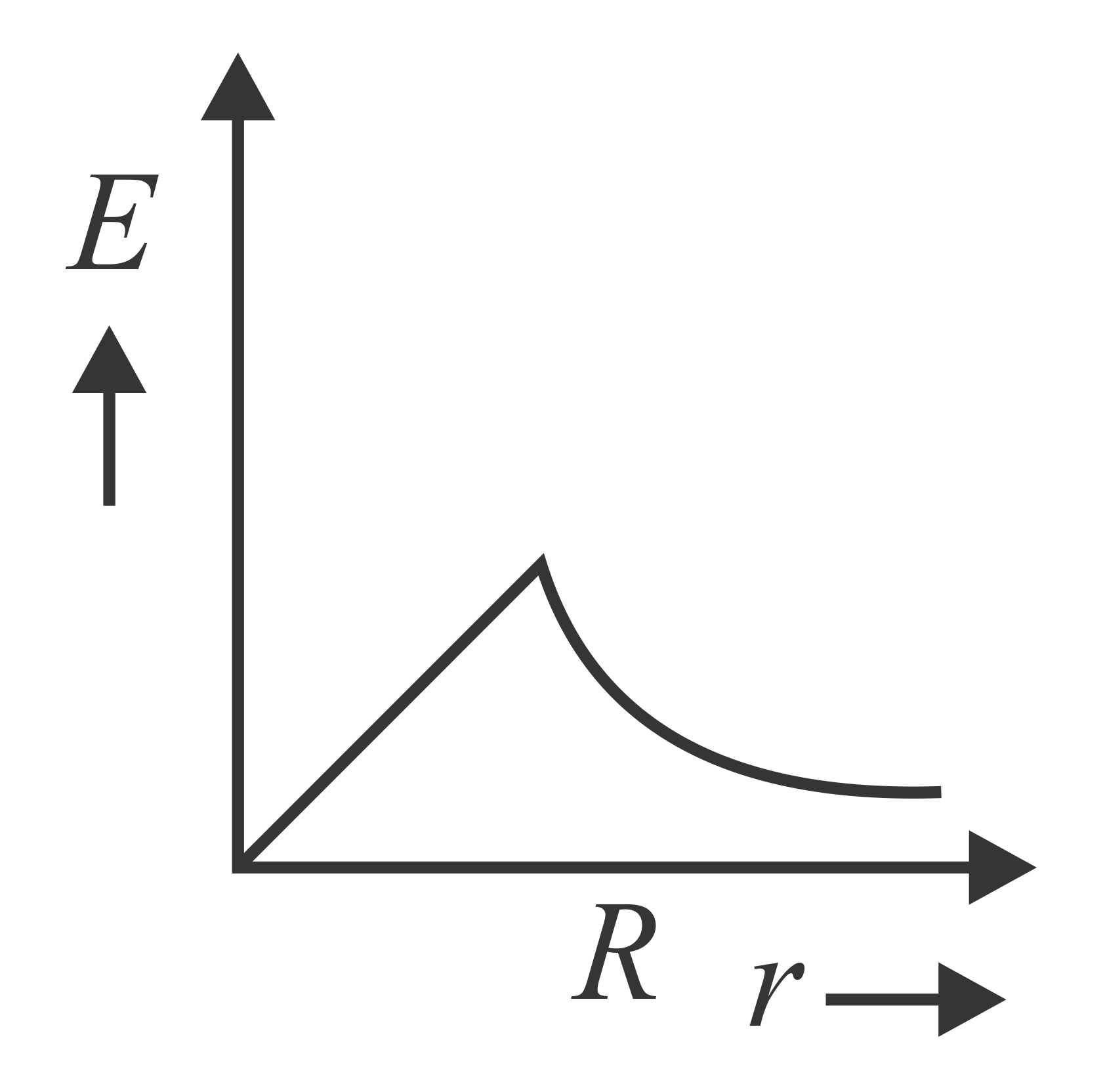
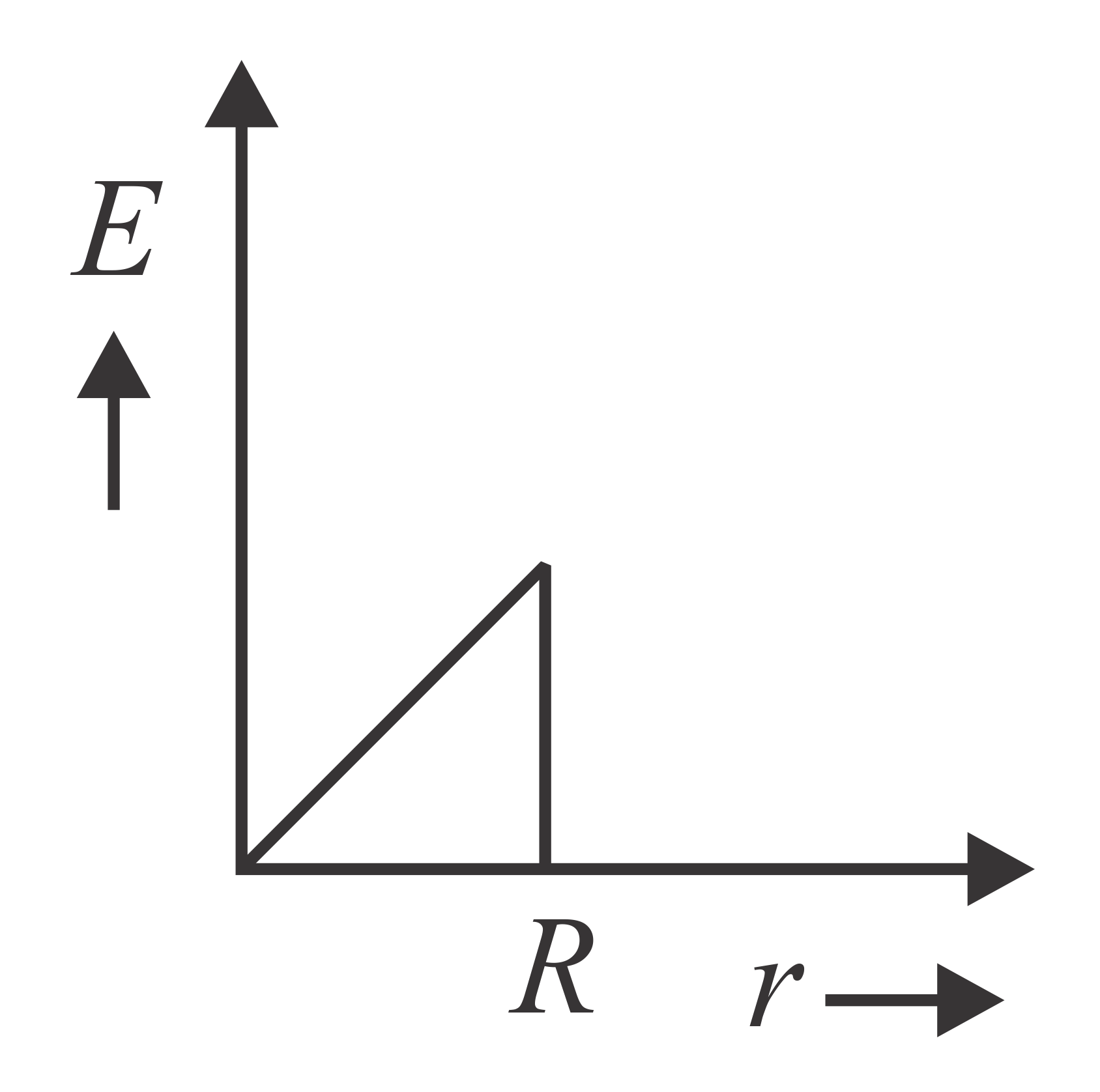
In a uniformly charged sphere of total charge $Q$ and radius $R$, the electric field $E$ is plotted as function of distance from the centre. The graph which would correspond to the above will be

This questions has Statement $1$ and Statement $2.$ Of the four choices given after the statements, choose the one that best describes the two statements.

An insulating solid sphere of radius $R$ has a uniformly positive charge density $\rho .$ As a result of this uniform charge distribution there is a finite value of the electric potential at the centre of the sphere, at the surface of the sphere and also at a point outside the sphere. The electric potential at infinity is zero.

Statement $1$: When a charge is taken from the centre to the surface of the sphere its potential energy changes by $\frac{q\rho }{3{\epsilon }_0}$
Statement $2$: The electric field at a distance $r(r<R)$ from the centre of the sphere is $\frac{\rho r}{3{\epsilon }_0}$

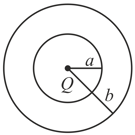
The region between two concentric spheres of radii $a$ and $b$, respectively (see figure) has a volume charge density $\rho = \frac{A}{r},$ where $A$ is a constant and $r$ is the distance from the centre. At the centre of the spheres is a point charge $Q$. The value of $A$ such that the electric field in the region between the spheres is constant is

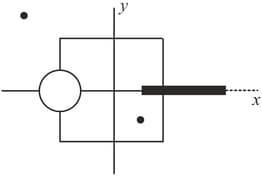
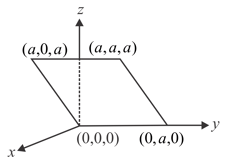
A disc of radius $\frac{a}{4}$ having a uniformly distributed charge of $6 \mathrm{C}$ is placed in the $xy$ plane with its centre at $\left(\frac{-a}{2}, 0, 0\right)$. A rod of length carrying a uniformly distributed charge $8 \mathrm{C}$ is placed on the $x$- axis  from $x = \frac{a}{4}$ to $x\mathit{ }=\frac{5a}{4}$. Two point charges $-7 \mathrm{C}$ and $3 \mathrm{C}$ are placed at $\left(\frac{a}{4}, \frac{-a}{4}, 0\right)$ and $\left(-\frac{3a}{4}, \frac{3a}{4}, 0\right)$ respectively. Consider a cubical surface formed by six surfaces $x= \pm \frac{a}{2}, y = \pm \frac{a}{2}, z= \pm \frac{a}{2}.$The electric flux through this cubical surface is 

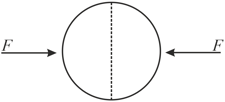
A uniformly charged spherical shell of radius $R$ carries a uniform charge density of $\sigma$ per unit area. It is made of two hemispherical shells, held together by pressing them with force $F$. $F$ is proportional to 

Consider electric field $\overrightarrow{E} = E_0\hat{x}$, where $E_0$ is a constant. The flux through the shaded area (as shown in the figure) due to this field is:

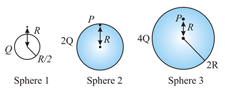
Charges $Q, 2Q , 4Q$ are uniformly distributed in three dielectric solid spheres $1, 2, 3$ of radii $\frac{R}{2}, R$ and $2R$  respectively , as shown in the figure. If magnitudes of the electric fields at point $P$ at a distance $R$ from the centres of spheres $1, 2 \text{and} 3$ are $E_1, E_2, E_3$ respectively, then :