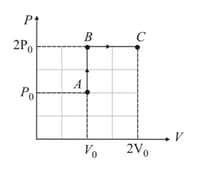
In given $\mathrm{P}-\mathrm{V}$ diagram, if the temperature of point $\mathrm{A}$ is ${\mathrm{T}}_0$, find the temperature at point $\mathrm{B}$ and $\mathrm{C}$. Also, draw $\mathrm{P}-\mathrm{T}$ and $\mathrm{V}-\mathrm{T}$ diagrams of given process.

 

In given $\mathrm{P}-\mathrm{V}$ diagram, the temperature at point $\mathrm{A}$ is ${\mathrm{T}}_0$, draw $\mathrm{P}-\mathrm{T}$ and $\mathrm{V}-\mathrm{T}$ diagram of given process.

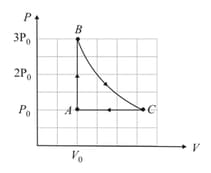
A cyclic process $\mathrm{ABCD}$, shown in $\mathrm{V}-\mathrm{T}$ diagram, is performed with a constant mass of an ideal gas. Show the same process on a $\mathrm{P}-\mathrm{V}$ diagram.

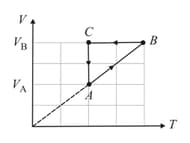
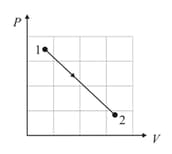
The diagrams given depict two different processes for a given mass of an ideal gas. What inference can be drawn regarding the change of pressure and volume of the gas from Figs. $\left(\mathrm{a}\right)$ and $\left(\mathrm{b}\right)$ respectively?

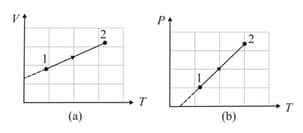
The diagram depicts variation of volume with pressure for a given mass of an ideal gas. What inference can be drawn regarding the change of temperature of the gas from point $1$ to point $2$ ?

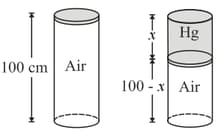
A metre long narrow bore held horizontally (and closed at one end) contains a $76 \mathrm{cm}$ long mercury thread, which traps a $15 \mathrm{cm}$ column of air. What happens if the tube is held vertically with the open end at the bottom?

A vertical cylindrical tank, $1 \mathrm{m}$ high, has its top end closed by a tightly fitted frictionless piston of negligible weight. The air inside the cylinder is an absolute pressure of $1 \mathrm{atm}$. The piston is depressed by pouring mercury on it very slowly. How far will the piston descend before mercury spills over the top of cylinder? The temperature of the air inside the cylinder is maintained constant.

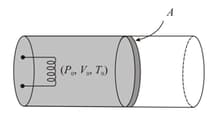
An ideal gas is filled in cylinder which is fitted with a movable non-conducting piston as shown in the figure. The gas in the cylinder is heated slowly. The gas expands and piston moves towards right. If the temperature of the gas increased slowly from ${\mathrm{T}}_0$ to $2{\mathrm{T}}_0$, find the displacement of the piston. (Given atmospheric pressure $={\mathrm{P}}_0$ and area of cross-section of the cylinder $=\mathrm{A}$ )

.

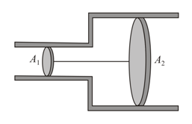
The figure shows a horizontal cylinder with two sections of unequal cross-section in which two points of area ${\mathrm{A}}_1$ and ${\mathrm{A}}_2$ can move freely. The pistons are joined together with an inextensible string and the space between the pistons is filled with an ideal gas. The whole system is in equilibrium.

If the atmospheric pressure is ${\mathrm{p}}_0$, then determine the pressure of the gas.