HARD

Earn 100

In radius of a circle which is inscribed in a isosceles triangle one of whose angle is $2 π / 3,$ is $\sqrt{3},$ then area of triangle (in sq units) is

50% studentsanswered this correctly

Important Questions on Properties of Triangle

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

Let

x, y

and

z

be positive real numbers. Suppose

x, y

and

z

are the lengths of the sides of a triangle opposite to its angles

X, Y

and

Z

respectively. If

\tan \frac{X}{2} + \tan \frac{Z}{2} = \frac{2 y}{x + y + z}

, then which of the following statements is/are TRUE?

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

Let

X, Y, Z

be respectively the areas of a regular pentagon, regular hexagon and regular heptagon which are inscribed in a circle of radius

1

. Then

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

In a $Δ A B C$ , points $X$ and $Y$ are on $A B$ and $A C$ , respectively, such that $X Y$ is parallel to $B C$ . Which of the two following equalities always hold? (Here, $[P Q R]$ denotes the area of $Δ P Q R$ ).

$I$ . $[B C X] = [B C Y]$

$II$ . $[A C X] \cdot [A B Y] = [A X Y] \cdot [A B C]$

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

Let

A B C

be a triangle such that

A B = 4, B C = 5

and

C A = 6

. Choose points

D, E, F

A B, B C, C A

respectively, such that

A D = 2, B E = 3, C F = 4

. Then

\frac{area Δ D E F}{area Δ A B C}

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

Let

A B C D

be a square and let

P

be point on segment

C D

such that

D P : P C = 1 : 2

. Let

Q

be a point on segment

A P

such that

∠ B Q P = 90^{o}

. Then the ratio of the area of quadrilateral

P Q B C

to the area of the square

A B C D

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

With usual notations, in

∆ A B C

, if

b \cos^{2} \frac{C}{2} + c \cos^{2} \frac{B}{2} = \frac{3 a}{2}

, then

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

In the figure given below, if the areas of the two regions are equal then which of the following is true?

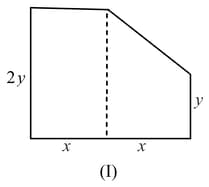
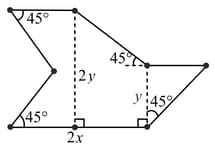
Question Image

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

Let

A B C D

be a convex cyclic quadrilateral. Suppose

P

is a point in the plane of the quadrilateral such that sum of its distances from the vertices of

A B C D

is the least. If

{P A, P B, P C, P D} = \{3, 4, 6, 8\}

, what is the maximum possible area of

A B C D ?

EASY

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

If the sides of triangle are

4, 5

and

6 cm

.

Then the area (in sq cm) of triangle is

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

Suppose we have two circles of radius $2$ each in the plane such that the distance between their centres is $2 \sqrt{3}$ . The area of the region common to both circles lies between

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

ΔABC,

the lengths of sides

A C

and

A B

are

12 cm

and

5 cm,

respectively. If the area of

∆ ABC

30 {cm}^{2}

and

R

and

r

are respectively the radii of circumcircle and incircle of

ΔABC

, then the value of

2 R + r (in cm)

is equal to ______ .

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

In the figure given below, $A B C D E F$ is a regular hexagon of side length $1$ unit, $A F P S$ and $A B Q R$ are squares. Then the ratio $\frac{area of △ A P Q}{area of △ S R P}$ equals

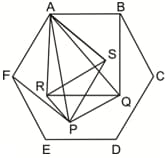
Question Image

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

In a quadrilateral

A B C D,

it is given that

A B = A D = 13, B C = C D = 20, B D = 24 .

r

is the radius of the circle inscribable in the quadrilateral, then what is the integer closest to

r ?

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

If in a triangle

A B C, a^{2} + 2 b c - (b^{2} + c^{2}) = a b \sin \frac{C}{2} \cos \frac{C}{2}

, then

\cot (B + C) =

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

15

and

9

are lengths of two medians of a triangle, what is the maximum possible area of the triangle to the nearest integer?

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

A triangle

A B C

has area of

P

square units and circumference

2 S

units. If

h_{1}, h_{2}

and

h_{3}

are respectively the length of the altitudes of the triangle drawn from the vertices

A, B

and

C,

then

P^{2} [\frac{{(h_{1} h_{2} + h_{2} h_{3} + h_{3} h_{1})}^{2}}{h_{1}^{2} h_{2}^{2} h_{3}^{2}} - 2] =

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

In a

∆ A B C,

a = 2 x, b = 2 y

and

∠ C = 120 °,

then the area of the triangle is

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

Consider four triangles having sides

(5, 12, 9), (5, 12, 11), (5, 12, 13)

and

(5, 12, 15)

. Among these the triangle having maximum area has sides

HARD

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

In a rectangle

A B C D,

points

X

and

Y

are the mid-points of

A D

and

D C

respectively. Lines

B X

and

C D

when extended intersect at

E

and lines

B Y

and

A D

when extended intersect at

F

. If the area of rectangle

A B C D

60

square units, then the area of

△ B E F

(in square units) is

MEDIUM

Mathematics>Trigonometry>Properties of Triangle>Half-Angle Formula and the Area of a Triangle

In a

∆ A B C

, if

\tan \frac{A}{2} = \frac{5}{6}, \tan \frac{C}{2} = \frac{2}{5}

, then

In radius of a circle which is inscribed in a isosceles triangle one of whose angle is 2π/3, is 3, then area of triangle (in sq units) is

Important Questions on Properties of Triangle

Learn and Prepare for any exam you want !

In radius of a circle which is inscribed in a isosceles triangle one of whose angle is $2 π / 3,$ is $\sqrt{3},$ then area of triangle (in sq units) is